题目内容
5.一元二次方程x2+x+m=0与mx2+x+1=0都有两不相等的实数根,且其中有一个公共的实根x0,那么m=-2.分析 先根据一元二次方程解的定义得到x02+x0+m=0与mx02+x0+1=0,把两方程相减得(m-1)x02=m-1,可解得x0=1或x0=-1,然后把它们分别代入计算求出满足条件的m的值.
解答 解:根据题意得x02+x0+m=0与mx02+x0+1=0,
所以(m-1)x02=m-1,
所以m-1≠0,解得x0=1或x0=-1,
当x0=1时,1+1+m=0,解得m=-2,
当x0=-1时,1-1+m=0,解得m=0(舍去),
所以m的值为-2.
故答案为-2.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目

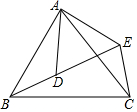 如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.
如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.