题目内容
2.如图,在平面直角坐标系中,直线AB:y=-$\frac{1}{3}$x+b交y轴于点A(0,1),交x轴于点B,直线x=1交x轴于点E,其中P(1,n)是直线x=1上一动点.(1)求直线AB的表达式和点B的坐标;
(2)如图1,当n=4时,过点P作PF⊥y轴于点F,连接PA,试说明△AOB≌△PFA;
(3)如图2,连接OP,BP.
①当n=$\sqrt{5}$时,判断△OBP的形状,并说明理由;
②是否存在实数n,使△OBP为直角三角形?若存在,求出n的值;若不存在,说明理由.

分析 (1)把A的坐标代入直线AB的解析式,即可求得b的值,根据x轴上当的坐标特征求出点B的坐标;
(2)根据全等三角形的判定定理证明即可;
(3)①根据勾股定理分别求出PB、AP、OB的长,根据等腰三角形的判定定理解答;
②根据直角三角形的判定定理列出关于n的方程,解方程即可.
解答 解:(1)∵y=-$\frac{1}{3}$x+b经过A(0,1),
∴b=1,
∴直线AB的解析式是y=-$\frac{1}{3}$x+1,
当y=0时,-$\frac{1}{3}$x+1=0,
解得,x=3,
则点B的坐标为:(3,0);
(2)当n=4时,AF=OF-OA=3,PF=OA=1,
在△AOB和△PFA中,
$\left\{\begin{array}{l}{OA=FP}\\{∠AOB=∠PFA}\\{OB=AF}\end{array}\right.$,
∴△AOB≌△PFA;
(3)①当n=$\sqrt{5}$时,
由勾股定理得,PB=$\sqrt{P{E}^{2}+B{E}^{2}}$=3,AP=$\sqrt{O{E}^{2}+P{E}^{2}}$=$\sqrt{6}$,
∴OB=PB,即△OBP是等腰三角形;
②当△OBP为直角三角形时,
由射影定理得,PE2=OE•BE,即n2=1×2,
解得,n=$±\sqrt{2}$,
则当n=$±\sqrt{2}$时,△OBP为直角三角形.
点评 本题考查的是待定系数法求函数解析式、全等三角形的判定、等腰三角形的判定以及直角三角形的判定,灵活运用待定系数法、掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
11.下列各数中,是负数的是( )
| A. | -(-5) | B. | |-5| | C. | (-5)2 | D. | -52 |
 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,找出图中相等的角,并说明理由.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,找出图中相等的角,并说明理由.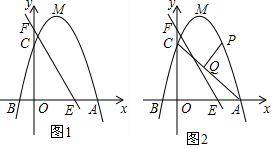

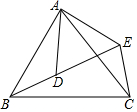 如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.
如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.