题目内容
14.已知-$\frac{1}{2}$<m<3,化简2m-$\sqrt{4{m}^{2}+m+1}$-$\sqrt{{m}^{2}-6m+9}$.分析 根据二次根似的性质化简二次根式,可得答案.
解答 解:2m-$\sqrt{4{m}^{2}+m+1}$-$\sqrt{{m}^{2}-6m+9}$=2m-$\sqrt{(2m+1)^{2}}$-$\sqrt{(m-3)^{2}}$,
∵-$\frac{1}{2}$<m<3,
∴原式=2m-(2m+1)-(3-m)
=2m-2m-1-3+m
=m-4.
点评 本题考查了二次根式的性质与化简,利用二次根式的性质化简是解题关键.

练习册系列答案
相关题目
2.在有理数在数轴上的位置如图所示,则下列各式的符号为负的是( )


| A. | -a-b | B. | a+b | C. | -a3b3 | D. | a4b4 |
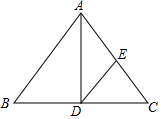 如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E.求证△AED是等腰三角形.
如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E.求证△AED是等腰三角形.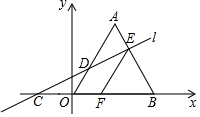 如图,在平面直角坐标系中,△AOB是边长为6的等边三角形,直线l与x轴、OA、AB分别交于点C、D、E,OC=AE.过点E作EF∥OA,交x轴于点F.
如图,在平面直角坐标系中,△AOB是边长为6的等边三角形,直线l与x轴、OA、AB分别交于点C、D、E,OC=AE.过点E作EF∥OA,交x轴于点F.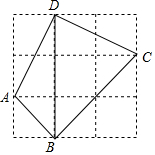 如图,在3×3的正方形网格中有一个四边形ABCD,若小正方形的边长为1,则sin∠ADB+cos∠DBC=$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{2}}{2}$.
如图,在3×3的正方形网格中有一个四边形ABCD,若小正方形的边长为1,则sin∠ADB+cos∠DBC=$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{2}}{2}$.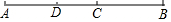 如图:C为线段AB的中点,D为线段AC的中点,解答下列问题:
如图:C为线段AB的中点,D为线段AC的中点,解答下列问题: 如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD绕着C点顺时针旋转50度与△ECB重合.
如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD绕着C点顺时针旋转50度与△ECB重合.