题目内容
3.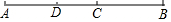 如图:C为线段AB的中点,D为线段AC的中点,解答下列问题:
如图:C为线段AB的中点,D为线段AC的中点,解答下列问题:(1)若AD+AC+AB=28,求线段BC的长度;
(2)若E是线段BC上的一点,M是线段EB的中点,DM=a,CE=b.求线段AB的长度(用含a,b的代数式表示)
分析 (1)根据终点的性质,可用BC表示AB,AD,DC,根据线段的和差,可得关于BC的方程,根据解方程,可得答案;
(2)根据线段中点的性质,可得BC的长,根据线段的和差,可得BE的长,根据线段中点的性质,可得EM的长,根据线段的和差,可得答案.
解答 解:(1)由C为线段AB的中点,D为线段AC的中点,得
AB=2BC,AC=BC,AD=$\frac{1}{2}$AC=$\frac{1}{2}$BC.
由AD+AC+AB=28,得
2BC+BC+$\frac{1}{2}$BC=28,
解得BC=8,
线段BC的长度8.
(2)如图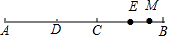 ,
,
设AD=DC=c,则BC=2c,由CE=b,
∴BE=2c-b.
∵M是线段EB的中点,
∴EM=$\frac{1}{2}$BE=c-$\frac{b}{2}$.
∵DE=DC+CE+EM,即a=c+b+c-$\frac{b}{2}$,
∴c=$\frac{a}{2}$-$\frac{b}{4}$,
∴AB=4c=2a-b.
点评 本题考查了两点间的距离,利用线段中点的性质,线段的和差是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
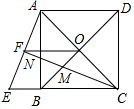 如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD,AE与点M,F,连接FO.
如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD,AE与点M,F,连接FO.
 如图所示的四边形ABCD中,AB∥CD,AD∥BC,你能用全等三角形的知识证明出AB=CD吗?
如图所示的四边形ABCD中,AB∥CD,AD∥BC,你能用全等三角形的知识证明出AB=CD吗?