题目内容
9.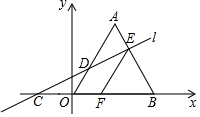 如图,在平面直角坐标系中,△AOB是边长为6的等边三角形,直线l与x轴、OA、AB分别交于点C、D、E,OC=AE.过点E作EF∥OA,交x轴于点F.
如图,在平面直角坐标系中,△AOB是边长为6的等边三角形,直线l与x轴、OA、AB分别交于点C、D、E,OC=AE.过点E作EF∥OA,交x轴于点F.(1)点A的坐标为(3,3$\sqrt{3}$)(结果保留根号)
(2)求证:CO=OF;
(3)若AD=EF,求直线l对应的函数表达式.
分析 (1)如图1中,作AM⊥OB于M.求出OM、AM即可解决问题.
(2)如图2中,作EN∥OB交OA于N.首先证明△AEN是等边三角形,再证明四边形ONEF是平行四边形即可解决问题.
(3)首先证明AN=OD=DN=AE=2,推出D(1,$\sqrt{3}$),E(4,2$\sqrt{3}$),设直线l的解析式为y=kx+b,则有$\left\{\begin{array}{l}{k+b=\sqrt{3}}\\{4k+b=2\sqrt{3}}\end{array}\right.$,解方程组即可解决问题.
解答 解:(1)如图1中,作AM⊥OB于M.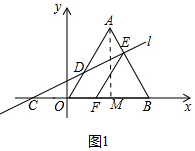
∵OA=AB,AM⊥OB,
∴OM=BM=3,AM=$\sqrt{O{A}^{2}-O{M}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴点A坐标为(3,3$\sqrt{3}$).
故答案为(3,3$\sqrt{3}$)
(2)如图2中,作EN∥OB交OA于N.
∵△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵EN∥OB,
∴∠ANE=∠AOB=60°,∠AEN=∠ABO=60°,∠DNE=∠COD,
∴△AEN是等边三角形,
∴AE=EN=CO,
∵EN∥OF,EF∥ON,
∴四边形ONEF是平行四边形,
∴OF=EN=OC,
∴CO=OF.
(3)如图2中,在△DNE和△DOC中,
$\left\{\begin{array}{l}{∠DNE=∠DOC}\\{∠NDE=∠ODC}\\{EN=OC}\end{array}\right.$,
∴△DNE≌△DOC,
∴DN=OD,
∵AD=EF=ON,
∴AN=OD=DN=AE=2,
∴D(1,$\sqrt{3}$),E(4,2$\sqrt{3}$),设直线l的解析式为y=kx+b,则有$\left\{\begin{array}{l}{k+b=\sqrt{3}}\\{4k+b=2\sqrt{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$.
点评 本题考查一次函数的应用、等边三角形的性质,平行四边形的判定和性质,待定系数法等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

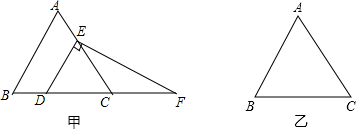
 如图,已知三角形纸片ABC,将它沿着经过点A的直线AD进行翻折,点C恰好落在线段AB上的点C1处.
如图,已知三角形纸片ABC,将它沿着经过点A的直线AD进行翻折,点C恰好落在线段AB上的点C1处.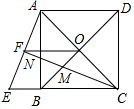 如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD,AE与点M,F,连接FO.
如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD,AE与点M,F,连接FO.