题目内容
 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A、c>-1 |
| B、9a+c>3b |
| C、2a+b≠0 |
| D、b>0 |
考点:二次函数图象与系数的关系
专题:
分析:根据抛物线与y轴的交点,可得c<-1,当x=-3时,y>0;对称轴在y轴的右侧,可得出b<0,从而可得出答案.
解答:解:由图象得,抛物线与y轴的交点,可得c<-1,故A错误;
当x=-3时,y=9a-3b+c>0,即9a+c>3b,故B正确;
∵对称轴为直线x=
=1,故C错误;
由对称轴在y轴的右侧,a与b异号,∴b<0,故D错误;
故选B.
当x=-3时,y=9a-3b+c>0,即9a+c>3b,故B正确;
∵对称轴为直线x=
| -2+4 |
| 2 |
由对称轴在y轴的右侧,a与b异号,∴b<0,故D错误;
故选B.
点评:本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标;当b2-4ac>0,抛物线与x轴有两个交点.
| b |
| 2a |

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.
甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.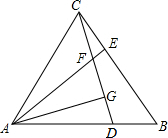 如图,等边△ABC中,D,E分别为AB,BC边上的点,且BD=CE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D,E分别为AB,BC边上的点,且BD=CE,AE与CD交于点F,AG⊥CD于点G.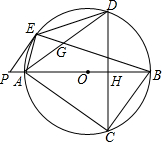 如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
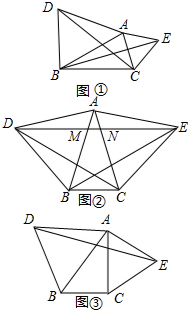 (1)如图①,在△ABC中,分别以AB,AC为边作等边△ABD和等边△ACE,猜想CD与BE有什么样的数量关系,直接写出结论,不需证明;
(1)如图①,在△ABC中,分别以AB,AC为边作等边△ABD和等边△ACE,猜想CD与BE有什么样的数量关系,直接写出结论,不需证明;