题目内容
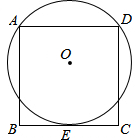如图，正方形ABCD的边BC与⊙O相切于点E，点A、D在⊙O上．若AB=10，则⊙O的半径是考点：切线的性质
专题：
分析：利用切线的性质以及垂径定理的性质得出FD=5，再利用勾股定理求出圆的半径长．
解答：
解：连接EO，并延长到AD上一点F，设⊙O的半径为x，
∵AB=10，正方形ABCD的边BC与⊙O相切于点E，
∴DO=x，FO=10-x，FD=5，
故在Rt△FOD中，
DO2=FD2+FO2，
即x2=52+（10-x）2，
解得：x=6.25，
即⊙O的半径是：6.25．
故答案为：6.25．
解：连接EO，并延长到AD上一点F，设⊙O的半径为x，∵AB=10，正方形ABCD的边BC与⊙O相切于点E，
∴DO=x，FO=10-x，FD=5，
故在Rt△FOD中，
DO2=FD2+FO2，
即x2=52+（10-x）2，
解得：x=6.25，
即⊙O的半径是：6.25．
故答案为：6.25．
点评：此题主要考查了切线的性质以及勾股定理等知识，正确利用勾股定理是解题关键．
练习册系列答案
一线名师权威作业本系列答案
相关题目
甲乙两人在同一条道路上同时出发，同时行进，甲步行，乙骑车，出发时甲在前，乙在后，图中l甲，l乙，分别表示出发后甲、乙离出发地的路程s（km）和经历的时间t（h）的关系．
已知：如图，AB是⊙O直径，弦CD⊥AB，E为CD延长线上一点，连结BE交圆于F．求证：CF•DE=BC•EF．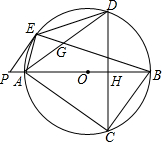
如图，点O是四边形AEBC外接圆的圆心，点O在AB上，点P在BA的延长线上，且∠PEA=∠ADE，CD⊥AB于点H，交⊙O于点D．
如图，△ADC内接于⊙O，且∠EAC=∠D，求证；AE是⊙O的切线．