题目内容
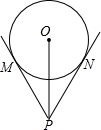 一个钢管放在V型架内,其截面如图,O为钢管界面圆的圆心,若PM=25
一个钢管放在V型架内,其截面如图,O为钢管界面圆的圆心,若PM=25| 3 |
| A、50cm | ||
B、25
| ||
| C、20cm | ||
| D、25cm |
考点:切线的性质
专题:应用题
分析:连接OM,由切线的性质和切线长定理得出∠OMP=90°,∠OPM=
∠MPN=30°,再运用锐角三角函数tan∠OPM=
=
,即可求出OM.
| 1 |
| 2 |
| OM |
| PM |
| OM | ||
25
|
解答:解:连接OM;如图所示:
∵PM、PN是⊙O的切线,
∴OM⊥PM,∠OPM=
∠MPN=30°,
∵tan∠OPM=
=
,
∴OM=25
•tan30°=25
•
=25;
即⊙O的半径为25cm;
故选:D.

∵PM、PN是⊙O的切线,
∴OM⊥PM,∠OPM=
| 1 |
| 2 |
∵tan∠OPM=
| OM |
| PM |
| OM | ||
25
|
∴OM=25
| 3 |
| 3 |
| ||
| 3 |
即⊙O的半径为25cm;
故选:D.
点评:本题考查了切线的性质和切线长定理以及锐角三角函数;由切线长定理得出∠OPM=30°是解决问题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
线段AB=6cm,BC=2cm,则A、C两点间的距离D是( )
| A、D=8cm |
| B、D=4cm |
| C、D=8cm或D=4cm |
| D、4cm≤D≤8cm |
已知等腰△ABC内接于半径为5的⊙O,如果底边BC的长为6,则底角的正切值为( )
| A、3 | ||||
B、
| ||||
C、3或
| ||||
D、3或
|
抛物线y=2+6x-x2的顶点坐标为( )
| A、(3,11) | ||||
| B、(-3,-25) | ||||
C、(
| ||||
| D、(6,2) |
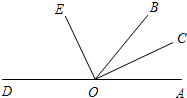 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,∠COE=( )°.
如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,∠COE=( )°.| A、60 | B、70 |
| C、90 | D、不能确定 |
 如图,直线AB与CD相交于点O,OE平分∠BOD.
如图,直线AB与CD相交于点O,OE平分∠BOD.