题目内容
1.解不等式组:$\left\{\begin{array}{l}{2-x>0}\\{\frac{3x+1}{2}>\frac{2x-1}{3}}\end{array}\right.$.分析 先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{2-x>0\;\;\;\;\;\;\;\;①}\\{\frac{3x+1}{2}>\frac{2x-1}{3}\;\;②}\end{array}\right.$
∵解不等式①得:x<2,
解不等式②得:x>-1,
在数轴上表示出来为:
∴不等式组的解集是:-1<x<2.
点评 本题考查了一元一次不等式组的解法,正确理解不等式组的解集的含义是关键.解一元一次不等式组的步骤:(1)求出这个不等式组中各个不等式的解集.(2)利用数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集.

练习册系列答案
相关题目
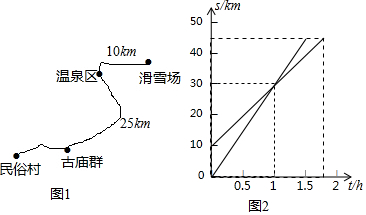
7.小李到农贸批发市场了解到苹果和西瓜的价格信息如下:
他共用280元批发了苹果和西瓜共75公斤,
(1)请问小李批发的苹果和西瓜各多少公斤?
(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱?
| 水果品种 | 苹果 | 西瓜 |
| 批发价格 | 8元/公斤 | 1.6元/公斤 |
| 零售价格 | 10元/公斤 | 2元/公斤 |
(1)请问小李批发的苹果和西瓜各多少公斤?
(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱?
14. 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1min仰卧起坐次数,并绘制如图所示的频数直方图,请根据图中的信息,计算仰卧起坐次数在25∽30次的百分比是( )
为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1min仰卧起坐次数,并绘制如图所示的频数直方图,请根据图中的信息,计算仰卧起坐次数在25∽30次的百分比是( )
 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1min仰卧起坐次数,并绘制如图所示的频数直方图,请根据图中的信息,计算仰卧起坐次数在25∽30次的百分比是( )
为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1min仰卧起坐次数,并绘制如图所示的频数直方图,请根据图中的信息,计算仰卧起坐次数在25∽30次的百分比是( )| A. | 40% | B. | 30% | C. | 20% | D. | 10% |
6. 将一副三角板如图1放置于桌面,其中30°、45°角共顶点,CM平分∠BCE,CN平分∠BCD,当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数是( )
将一副三角板如图1放置于桌面,其中30°、45°角共顶点,CM平分∠BCE,CN平分∠BCD,当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数是( )
 将一副三角板如图1放置于桌面,其中30°、45°角共顶点,CM平分∠BCE,CN平分∠BCD,当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数是( )
将一副三角板如图1放置于桌面,其中30°、45°角共顶点,CM平分∠BCE,CN平分∠BCD,当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数是( )| A. | 15° | B. | 22.5° | C. | 37.5° | D. | 无法确定 |
11.下列语句写成数学式子正确的是( )
| A. | 9是81的算术平方根:$±\sqrt{81}=9$ | B. | ±6是36的平方根:$\sqrt{36}=±6$ | ||
| C. | 5是(-5)2的算术平方根:$\sqrt{{{(-5)}^2}}=5$ | D. | -2是4的负的平方根:$\sqrt{-4}=-2$ |
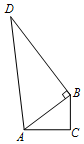 某机器零件呈四边形ACBD的形状,要求∠ABD=90°,∠C=90°.现测得∠ABD=90°,AD=39,BD=36,AC=12,BC=9.你认为这个零件合格吗?说明理由.
某机器零件呈四边形ACBD的形状,要求∠ABD=90°,∠C=90°.现测得∠ABD=90°,AD=39,BD=36,AC=12,BC=9.你认为这个零件合格吗?说明理由.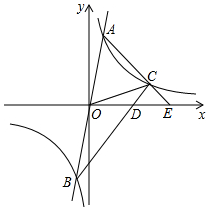 如图,双曲线y1=$\frac{k}{x}$与过原点的直线:y2=mx交于点A(1,4),B(-1,-4),
如图,双曲线y1=$\frac{k}{x}$与过原点的直线:y2=mx交于点A(1,4),B(-1,-4),