题目内容
10.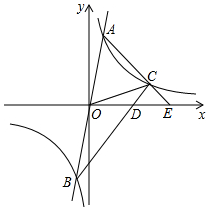 如图,双曲线y1=$\frac{k}{x}$与过原点的直线:y2=mx交于点A(1,4),B(-1,-4),
如图,双曲线y1=$\frac{k}{x}$与过原点的直线:y2=mx交于点A(1,4),B(-1,-4),(1)当y1<y2时,x的取值范围是-1<x<0或x>1;
(2)点C是双曲线y1=$\frac{k}{x}$(x>0)一点(不与A重合),直线AC、BC与x轴分别交于E、D;
①若OA=OC,则△CDE的面积为1
②若CE:CB=1:4,求△CDE的面积.
分析 (1)由图象可以直接得结论;
(2)①因为反比例函数是轴对称图形,由对称性可得C的坐标为(4,1),分别求直线BC和AC的解析式,可得DE的长,利用面积公式可得结果;
②先根据A的坐标表示反比例函数的解析式,设C(a,$\frac{4}{a}$)(a>0,且a≠1),作辅助线,构建直角三角形,利用勾股定理根据CE:CB=1:4,列等式可得a的值,从而计算其结果.
解答 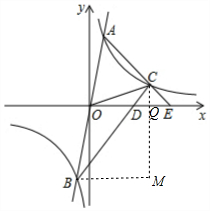 解:(1)∵曲线y1=$\frac{k}{x}$与过原点的直线y2=mx交于点A(1,4),B(-1,-4),
解:(1)∵曲线y1=$\frac{k}{x}$与过原点的直线y2=mx交于点A(1,4),B(-1,-4),
∴当y1<y2时,x的取值范围是:-1<x<0或x>1;
(2)①∵OA=OC,
由对称性得:C(4,1),
设直线BC的解析式为:y=kx+b,
把B(-1,-4)和C(4,1)代入得:$\left\{\begin{array}{l}{-k+b=-4}\\{4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为:y=x-3,
当y=0时,x-3=0,
x=3,
∴OD=3,
同理得AC的解析式为:y=-x+5,
当y=0时,-x+5=0,
x=5,
∴OE=5,
∴DE=5-3=2,
∴S△CDE=$\frac{1}{2}$×2×1=1;
故答案为:1;
②如图,过C作CQ⊥x轴于Q,过B作BM⊥y轴,BM与CQ交于M,
∵点A在反比例函数y=$\frac{k}{x}$上,
∴k=1×4=4,
∴反比例函数为:y=$\frac{4}{x}$,
设C(a,$\frac{4}{a}$)(a>0,且a≠1),
由勾股定理得:BC2=CM2+BM2,
$B{C}^{2}=(a+1)^{2}+(4+\frac{4}{a})^{2}$,
设AC:y=kx+b,
把A(1,4)和C(a,$\frac{4}{a}$)代入得:$\left\{\begin{array}{l}{k+b=4}\\{ak+b=\frac{4}{a}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{a}}\\{b=4+\frac{4}{a}}\end{array}\right.$,
∴AC:y=-$\frac{4x}{a}$+4+$\frac{4}{a}$,
当y=0时,-$\frac{4x}{a}$+4+$\frac{4}{a}$=0,
x=a+1,
∴OE=a+1,
∴EQ=a+1-a=1,
∴EQ2+CQ2=CE2=$(\frac{4}{a})^{2}$+1,
∵CE:CB=1:4,
∴BC=4CE,
∴BC2=16CE2,
∴(a+1)2+(4+$\frac{4}{a}$)2=16[$\frac{16}{{a}^{2}}$+1],
(a+1)2+$\frac{16(a+1)^{2}}{{a}^{2}}$=16[$\frac{16}{{a}^{2}}$+1],
(a+1)2($\frac{16}{{a}^{2}}$+1)=16[$\frac{16}{{a}^{2}}$+1],
∴(a+1)2=16,
a+1=±4,
a1=3,a2=-5(舍),
∴C(3,$\frac{4}{3}$),
易得BC的解析式为:y=$\frac{4}{3}$x-$\frac{8}{3}$,
当y=0时,$\frac{4}{3}$x-$\frac{8}{3}$=0,
x=2,
∴OD=2,
∴DE=OE-OD=3+1-2=2,
∴S△CDE=$\frac{1}{2}$×2×$\frac{4}{3}$=$\frac{4}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题、勾股定理、利用待定系数法求函数的解析式、函数与坐标轴的交点等知识,同时还运用了数形结合的思想,第二问有难度,注意第一小问的附加条件,只能单独运用.

| A. | 在标准大气压下,水加热到100°时沸腾 | |
| B. | 小明购买1张彩票,中奖 | |
| C. | 在一个装有红球和黄球的袋中,摸出蓝球 | |
| D. | 一名运动员的速度为30米/秒 |
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | 0 |
| A. | 等腰三角形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |