题目内容
6. 将一副三角板如图1放置于桌面,其中30°、45°角共顶点,CM平分∠BCE,CN平分∠BCD,当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数是( )
将一副三角板如图1放置于桌面,其中30°、45°角共顶点,CM平分∠BCE,CN平分∠BCD,当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数是( )| A. | 15° | B. | 22.5° | C. | 37.5° | D. | 无法确定 |
分析 根据角平分线的性质可得在图1中,∠MCN=$\frac{1}{2}$∠BCE+$\frac{1}{2}$∠BCD=$\frac{1}{2}$(∠BCE+∠BCD)=$\frac{1}{2}$∠DCE,在图2中,∠MCN=$\frac{1}{2}$∠BCD-$\frac{1}{2}$∠BCE=$\frac{1}{2}$(∠BCD-∠BCE)=$\frac{1}{2}$∠DCE,即可得答案.
解答 解:在图1中,
∵CM平分∠BCE,CN平分∠BCD,
∴∠MCN=$\frac{1}{2}$∠BCE+$\frac{1}{2}$∠BCD=$\frac{1}{2}$(∠BCE+∠BCD)=$\frac{1}{2}$∠DCE=$\frac{1}{2}$×30°=15°;
在图2中,
∠MCN=$\frac{1}{2}$∠BCD-$\frac{1}{2}$∠BCE=$\frac{1}{2}$(∠BCD-∠BCE)=$\frac{1}{2}$∠DCE=$\frac{1}{2}$30°=15°,
∴当三角板DEC从图1中位置绕着点C逆时针旋转到图2中的位置时,∠MCN度数保持不变为15°,
故选:A.
点评 本题主要考查了角的计算以及角平分线的性质.在两个图中得到∠MCN=$\frac{1}{2}$∠DCE是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
14.实数n、m是连续整数,如果n<$\sqrt{17}$<m,那么m+n的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
15.在实数$\sqrt{4}$,$\sqrt{3}$,$-\frac{17}{5}$,π,$0.\stackrel{•}9$,1.010010001…(每两个1之间0的个数依次加1)中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18.下列事件是随机事件的是( )
| A. | 在标准大气压下,水加热到100°时沸腾 | |
| B. | 小明购买1张彩票,中奖 | |
| C. | 在一个装有红球和黄球的袋中,摸出蓝球 | |
| D. | 一名运动员的速度为30米/秒 |
15.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
②按两种纸盒的生产个数来分,有哪几种生产方案?
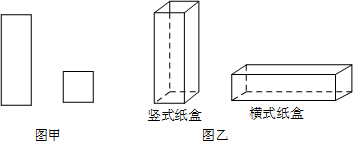
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |

 如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.
如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.