题目内容
 如图,已知抛物线y=x2-2x+m与x轴交于,B两点,与y轴交于点C(0,-3).
如图,已知抛物线y=x2-2x+m与x轴交于,B两点,与y轴交于点C(0,-3).(1)求抛物线的解析式;
(2)若在第四象限的抛物线上存在点P,使△PBC为以点C为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使四边形BCPQ为直角梯形?若存在,请求出Q的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把点C的坐标代入抛物线y=x2-2x+m求解即可,
(2)延长PC交x轴于点Q,先求出直线AC的解析式,再与抛物线的解析式联立求出P点的坐标即可,
(3)先求出PQ的解析式为y=x+b,再与抛物线的解析式联立求出Q点的坐标即可,
(2)延长PC交x轴于点Q,先求出直线AC的解析式,再与抛物线的解析式联立求出P点的坐标即可,
(3)先求出PQ的解析式为y=x+b,再与抛物线的解析式联立求出Q点的坐标即可,
解答:解:(1)∵抛物线y=x2-2x+m与y轴交于点C(0,-3).
∴m=-3,
∴抛物线的解析式为y=x2-2x-3.
(2)如图1,延长PC交x轴于点Q,
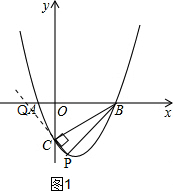
∵抛物线的解析式为y=x2-2x-3.
∴A(-1,0),B(3,0),
∴CO=BO,
∵∠PCB=90°,
∴∠CAB=45°,
∴直线AC的解析式为y=-x-3,
∴联立得
,解得
或
,
∴P(1,-4)或P(0,-3)(舍去)
(3)存在.Q(2,-3)
如图2,设PQ的解析式为y=x+b,
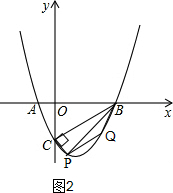
∵把点P(1,-4)代入得-4=1+b,解得b=-5,
∴直线y=x-5,
联立
,解得
或
,
∴Q(1,-4)(舍去)或(2,-3)
∴Q(2,-3).
∴m=-3,
∴抛物线的解析式为y=x2-2x-3.
(2)如图1,延长PC交x轴于点Q,

∵抛物线的解析式为y=x2-2x-3.
∴A(-1,0),B(3,0),
∴CO=BO,
∵∠PCB=90°,
∴∠CAB=45°,
∴直线AC的解析式为y=-x-3,
∴联立得
|
|
|
∴P(1,-4)或P(0,-3)(舍去)
(3)存在.Q(2,-3)
如图2,设PQ的解析式为y=x+b,

∵把点P(1,-4)代入得-4=1+b,解得b=-5,
∴直线y=x-5,
联立
|
|
|
∴Q(1,-4)(舍去)或(2,-3)
∴Q(2,-3).
点评:本题主要考查了二次函数的综合题,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
相关题目
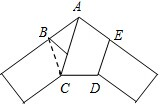 将固定宽度的纸条打一个简单的结,然后系紧,使它成为一个平面的结,如图所示,求证:这个五边形是正五边形.
将固定宽度的纸条打一个简单的结,然后系紧,使它成为一个平面的结,如图所示,求证:这个五边形是正五边形.
 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,BD=6,∠ACD=30°.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,BD=6,∠ACD=30°.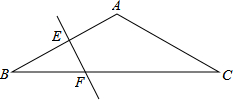 在△ABBC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,求证:BF=
在△ABBC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,求证:BF=