题目内容
（1）如图，AD是△ABC的角平分线，求证：
=
．
（2）如果AD是外角平分线，上面的结论是否成立？如果成立，请证明；如果不成立，请探究会有什么结论．
| AB |
| AC |
| BD |
| CD |
（2）如果AD是外角平分线，上面的结论是否成立？如果成立，请证明；如果不成立，请探究会有什么结论．
考点：平行线分线段成比例
专题：探究型
分析：（1）证明过C点作CE∥AD交BA的延长线于E，如图1，根据平行线的性质得到∠1=∠E，∠2=∠3，再利用AD是△ABC的角平分线得到∠1=∠2，则∠E=∠3，所以AE=AC，然后根据平行线分线段成比例定理得
=
，再利用等线段代换即可得到结论；
（2）过C点作CE∥AD交AB于E，如图2，证明方法与（1）一样可得到
=
．
| BA |
| AE |
| BD |
| CD |
（2）过C点作CE∥AD交AB于E，如图2，证明方法与（1）一样可得到
| AB |
| AC |
| BD |
| CD |
解答：（1）证明：
过C点作CE∥AD交BA的延长线于E，如图1，
∵CE∥AD，
∴∠1=∠E，∠2=∠3，
∵AD是△ABC的角平分线，
∴∠1=∠2，
∴∠E=∠3，
∴AE=AC，
∵AD∥CE，
∴
=
，
∴
=
；
（2）解：上面的结论成立．理由如下：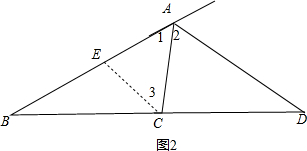
过C点作CE∥AD交AB于E，如图2，
∵CE∥AD，
∴∠2=∠3，
∵AD是△ABC的角平分线，
∴∠1=∠2，
∴∠1=∠3，
∴AE=EC，
∵AD∥CE，
∴
=
，
∴
=
．
过C点作CE∥AD交BA的延长线于E，如图1，∵CE∥AD，
∴∠1=∠E，∠2=∠3，
∵AD是△ABC的角平分线，
∴∠1=∠2，
∴∠E=∠3，
∴AE=AC，
∵AD∥CE，
∴
| BA |
| AE |
| BD |
| CD |
∴
| AB |
| AC |
| BD |
| CD |
（2）解：上面的结论成立．理由如下：
过C点作CE∥AD交AB于E，如图2，
∵CE∥AD，
∴∠2=∠3，
∵AD是△ABC的角平分线，
∴∠1=∠2，
∴∠1=∠3，
∴AE=EC，
∵AD∥CE，
∴
| BA |
| AE |
| BD |
| CD |
∴
| AB |
| AC |
| BD |
| CD |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
相关题目
下列式子中，次数为4的单项式是（ ）
| A、x2+y2 |
| B、x3y+y3 |
| C、3x2y |
| D、x2y2 |
为比较两条线段AB与CD的大小，小明将点A与点C重合使两条线段在一条直线上，点B在CD的延长线上，则（ ）
| A、AB＜CD |
| B、AB＞CD |
| C、AB=CD |
| D、以上都有可能 |
如图，已知抛物线y=x2-2x+m与x轴交于，B两点，与y轴交于点C（0，-3）．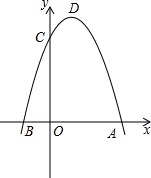
如图，二次函数y=-x2+2（m-2）x+3的图象与x，y轴交于A，B，C三点，其中A（3，0），抛物线的顶点为D．
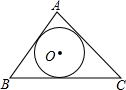已知，如图，在锐角△ABC中，tanB=