题目内容
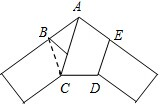将固定宽度的纸条打一个简单的结，然后系紧，使它成为一个平面的结，如图所示，求证：这个五边形是正五边形．考点：正多边形和圆
专题：证明题
分析：如图，作辅助线；证明OM=ON，此为解题的关键性结论；证明四边形AODE为平行四边形，得到AE=DE，即可解决问题．
解答：
证明：如图，连接BD；过点O作OM⊥AE、ON⊥DE；
则OM=ON；
∵AC∥DE，BD∥AE，
∴四边形AODE为平行四边形，
∴由四边形的面积公式得：
AE•OM=DE•ON，
∴AE=DE；同理可证：
AB=BC=CD=DE，
∴AB=BC=CD=DE=AE，
即该五边形为正五边形．
证明：如图，连接BD；过点O作OM⊥AE、ON⊥DE；则OM=ON；
∵AC∥DE，BD∥AE，
∴四边形AODE为平行四边形，
∴由四边形的面积公式得：
AE•OM=DE•ON，
∴AE=DE；同理可证：
AB=BC=CD=DE，
∴AB=BC=CD=DE=AE，
即该五边形为正五边形．
点评：该题主要考查了正多边形的判定问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断、解答．
练习册系列答案
阅读快车系列答案
相关题目
关于x的方程（m2-1）x2+x-2=0是一元二次方程，则m满足（ ）
| A、m≠1 | B、m≠-1 |
| C、m≠±1 | D、为任意实数 |
若|m|=2，|n|=4，且m＞0，n＜0，则m-n=（ ）
| A、-2 | B、2 | C、6 | D、-6 |
为比较两条线段AB与CD的大小，小明将点A与点C重合使两条线段在一条直线上，点B在CD的延长线上，则（ ）
| A、AB＜CD |
| B、AB＞CD |
| C、AB=CD |
| D、以上都有可能 |
如图，在△ABC中，∠B=90°，D在AC上，AD=AB=BC，DE⊥AC，垂足为D，求证：BE=DC．
如图，已知抛物线y=x2-2x+m与x轴交于，B两点，与y轴交于点C（0，-3）．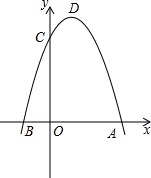
如图，二次函数y=-x2+2（m-2）x+3的图象与x，y轴交于A，B，C三点，其中A（3，0），抛物线的顶点为D．