题目内容
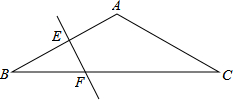 在△ABBC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,求证:BF=
在△ABBC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,求证:BF=| 1 |
| 2 |
考点:含30度角的直角三角形
专题:证明题
分析:连接AF,结合条件可得到∠B=∠C=30°,∠AFC=60°,再利用含30°直角三角形的性质即可得到AF=BF=
CF.
| 1 |
| 2 |
解答: 证明:连接AF,
证明:连接AF,
∵EF为AB的垂直平分线,
∴AF=BF,
又∵AB=AC,∠BAC=120°,
∴∠B=∠C=∠BAF=30°,
∴∠FAC=90°,
∴AF=
FC,
∴BF=
FC.
 证明:连接AF,
证明:连接AF,∵EF为AB的垂直平分线,
∴AF=BF,
又∵AB=AC,∠BAC=120°,
∴∠B=∠C=∠BAF=30°,
∴∠FAC=90°,
∴AF=
| 1 |
| 2 |
∴BF=
| 1 |
| 2 |
点评:本题主要考查垂直平分线的性质及等腰三角形的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若|m|=2,|n|=4,且m>0,n<0,则m-n=( )
| A、-2 | B、2 | C、6 | D、-6 |
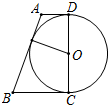 如图,已知梯形ABCD中,AD∥BC,∠C=90°,以CD为直径的圆与AB相切,AB=6,那么梯形ABCD的面积是( )
如图,已知梯形ABCD中,AD∥BC,∠C=90°,以CD为直径的圆与AB相切,AB=6,那么梯形ABCD的面积是( )| A、2 | B、3 |
| C、4 | D、不能确定,与∠B的大小有关 |
 如图,已知抛物线y=x2-2x+m与x轴交于,B两点,与y轴交于点C(0,-3).
如图,已知抛物线y=x2-2x+m与x轴交于,B两点,与y轴交于点C(0,-3).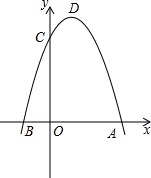 如图,二次函数y=-x2+2(m-2)x+3的图象与x,y轴交于A,B,C三点,其中A(3,0),抛物线的顶点为D.
如图,二次函数y=-x2+2(m-2)x+3的图象与x,y轴交于A,B,C三点,其中A(3,0),抛物线的顶点为D. 已知,如图,在锐角△ABC中,tanB=
已知,如图,在锐角△ABC中,tanB=