题目内容
 如图所示,抛物线y=ax2+bx+c的顶点为M(-2,-4),与x轴交于A、B两点,且A(-6,0),与x轴交于点C.
如图所示,抛物线y=ax2+bx+c的顶点为M(-2,-4),与x轴交于A、B两点,且A(-6,0),与x轴交于点C.(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据顶点坐标公式即可求得a、b、c的值,即可解题;
(2)易求得点B、C的坐标,即可求得OC的长,即可求得△ABC的面积,即可解题;
(3)作PE⊥x轴于点E,交AC于点F,可将△APC的面积转化为△AFP和△CFP的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示△APC的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
(2)易求得点B、C的坐标,即可求得OC的长,即可求得△ABC的面积,即可解题;
(3)作PE⊥x轴于点E,交AC于点F,可将△APC的面积转化为△AFP和△CFP的面积之和,而这两个三角形有共同的底PF,这一个底上的高的和又恰好是A、C两点间的距离,因此若设设E(x,0),则可用x来表示△APC的面积,得到关于x的一个二次函数,求得该二次函数最大值,即可解题.
解答:解:(1)设此函数的解析式为y=a(x+h)2+k,
∵函数图象顶点为M(-2,-4),
∴y=a(x+2)2-4,
又∵函数图象经过点A(-6,0),
∴0=a(-6+2)2-4
解得a=
,
∴此函数的解析式为y=
(x+2)2-4,即y=
x2+x-3;
(2)∵点C是函数y=
x2+x-3的图象与y轴的交点,
∴点C的坐标是(0,-3),
又当y=0时,有y=
x2+x-3=0,
解得x1=6,x2=2,
∴点B的坐标是(2,0),
则S△ABC=
|AB|•|OC|=
×8×3=12;
(3)假设存在这样的点,过点P作PE⊥x轴于点E,交AC于点F.
设E(x,0),则P(x,
x2+x-3),

设直线AC的解析式为y=kx+b,
∵直线AC过点A(-6,0),C(0,-3),
∴
,
解得
,
∴直线AC的解析式为y=-
x-3,
∴点F的坐标为F(x,-
x-3),
则|PF|=-
x-3-(
x2+x-3)=-
x2-
x,
∴S△APC=S△APF+S△CPF
=
|PF|•|AE|+
|PF|•|OE|
=
|PF|•|OA|=
(-
x2-
x)×6=-
x2-
x=-
(x+3)2+
,
∴当x=-3时,S△APC有最大值
,
此时点P的坐标是P(-3,-
).
∵函数图象顶点为M(-2,-4),
∴y=a(x+2)2-4,
又∵函数图象经过点A(-6,0),
∴0=a(-6+2)2-4
解得a=
| 1 |
| 4 |
∴此函数的解析式为y=
| 1 |
| 4 |
| 1 |
| 4 |
(2)∵点C是函数y=
| 1 |
| 4 |
∴点C的坐标是(0,-3),
又当y=0时,有y=
| 1 |
| 4 |
解得x1=6,x2=2,
∴点B的坐标是(2,0),
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)假设存在这样的点,过点P作PE⊥x轴于点E,交AC于点F.
设E(x,0),则P(x,
| 1 |
| 4 |

设直线AC的解析式为y=kx+b,
∵直线AC过点A(-6,0),C(0,-3),
∴
|
解得
|
∴直线AC的解析式为y=-
| 1 |
| 2 |
∴点F的坐标为F(x,-
| 1 |
| 2 |
则|PF|=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
∴S△APC=S△APF+S△CPF
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 4 |
| 27 |
| 4 |
∴当x=-3时,S△APC有最大值
| 27 |
| 4 |
此时点P的坐标是P(-3,-
| 15 |
| 4 |
点评:本题考查了抛物线解析式的求解,考查了一元二次方程的求解,考查了二次函数最值的求解,考查了二次函数的应用,本题中正确求得抛物线解析式是解题的关键.

练习册系列答案
相关题目
下列命题中,是假命题的是( )
| A、同弧所对的圆周角相等 |
| B、同圆中相等的圆周角所对的弧相等 |
| C、等弧所对的圆周角相等或互补 |
| D、同圆中等弦所对的圆周角相等 |
解方程组
,以下解法不正确的是( )
|
| A、由①,②消去z,再由①,③消去z |
| B、由①,③消去z,再由②,③消去z |
| C、由①,③消去y,再由①,②消去y |
| D、由①,②消去z,再由①,③消去y |
 小小的螺丝帽在日常生活中却有着很大的作用,常用的螺丝帽有六角螺丝和四角螺帽,请比较一下,制作同样厚度和宽度(指平行边间的距离)的这两种螺帽坯(如图),哪种用料少?两种螺帽毛坯用料的比例是多少?
小小的螺丝帽在日常生活中却有着很大的作用,常用的螺丝帽有六角螺丝和四角螺帽,请比较一下,制作同样厚度和宽度(指平行边间的距离)的这两种螺帽坯(如图),哪种用料少?两种螺帽毛坯用料的比例是多少?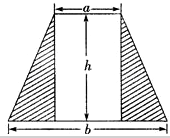 (1)用代数式表示图中阴影部分的面积S.
(1)用代数式表示图中阴影部分的面积S. 在平面直角坐标系中,规定把一个等边三角形先沿y轴翻折,再向上平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点A、B、C的坐标分别是A(-2,
在平面直角坐标系中,规定把一个等边三角形先沿y轴翻折,再向上平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点A、B、C的坐标分别是A(-2,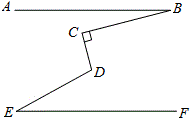 如图,AB∥EF,∠C=90°,试探究:∠B,∠CDE,∠E之间的数量关系,并说明理由.
如图,AB∥EF,∠C=90°,试探究:∠B,∠CDE,∠E之间的数量关系,并说明理由.