题目内容
1.已知13x2-6xy+y2-4x+1=0,求(x+y)2015•x2014的值.分析 把13x2分成9x2+4x2,然后分别与剩余的项组成完全平方形式,从而出现两个非负数的和等于0的形式,那么每一个非负数都等于0,从而求出x、y的值,再把x、y的值代入所求式子,计算即可.
解答 解:∵13x2-6xy+y2-4x+1=0,
∴9x2-6xy+y2+4x2-4x+1=0,
即(3x-y)2+(2x-1)2=0,
∴3x-y=0,2x-1=0,
解得x=$\frac{1}{2}$,y=$\frac{3}{2}$,
当x=$\frac{1}{2}$,y=$\frac{3}{2}$时,
∴(x+y)2015•x2014=($\frac{1}{2}$+$\frac{3}{2}$)2015•$\frac{1}{2}$2014=2.
点评 本题主要考查完全平方公式、非负数的性质.完全平方公式:(a±b)2=a2±2ab+b2.注意会正确的拆项.

练习册系列答案
相关题目
11.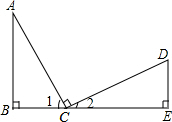 已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠1=∠2 |
10.反比例函数y=$\frac{m-3}{x}$的图象,当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
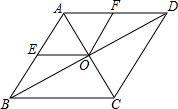 平行四边形ABCD的对角线AC,BD相交于点O,AE=EB,OF=$\frac{1}{2}$CD,求证:四边形AEOF为平行四边形.
平行四边形ABCD的对角线AC,BD相交于点O,AE=EB,OF=$\frac{1}{2}$CD,求证:四边形AEOF为平行四边形.