题目内容
 如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为
如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为考点:相似三角形的判定
专题:
分析:本题应分两种情况进行讨论,①△ABC∽△AED;②△ABC∽△ADE;可根据各相似三角形得出的关于AE、AE、AB、AC四条线段的比例关系式求出AE的长.
解答:解:本题分两种情况:
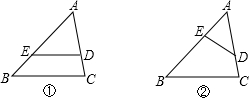
①△ADE∽△ACB
∴AB:AC=AE:AD,
∵AB=12,AC=9,AD=6,
∴AE=8;
②△ADE∽△ABC
∴AB:AC=AD:AE,
∵AB=12,AC=9,AD=6,
∴AE=4.5,
故答案为:8或4.5.

①△ADE∽△ACB
∴AB:AC=AE:AD,
∵AB=12,AC=9,AD=6,
∴AE=8;
②△ADE∽△ABC
∴AB:AC=AD:AE,
∵AB=12,AC=9,AD=6,
∴AE=4.5,
故答案为:8或4.5.
点评:本题主要考查了相似三角形的性质.由于题中没有明确相似三角形的对应角和对应边,因此本题要分情况进行讨论,以免漏解.

练习册系列答案
相关题目
 如图中的同旁内的角共有( )
如图中的同旁内的角共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
下列条件中,不能判定两个直角三角形全等的是( )
| A、两个锐角对应相等 |
| B、一条边和一个锐角对应相等 |
| C、两条直角边对应相等 |
| D、一条直角边和一条斜边对应相等 |
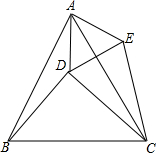 如图,△ABC是等边三角形,△BDC是等腰直角三角形,∠BDC=90°,连接AD,以AD为边作等边△ADE,连接CE.
如图,△ABC是等边三角形,△BDC是等腰直角三角形,∠BDC=90°,连接AD,以AD为边作等边△ADE,连接CE.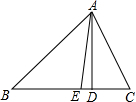 己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC.
己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,求△AEF的周长.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,求△AEF的周长.