题目内容
 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,求△AEF的周长.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,求△AEF的周长.考点:矩形的性质,勾股定理,三角形中位线定理
专题:
分析:由勾股定理可先求得AC,再结合中点的定义及中位线的性质可分别求得AE、AF、EF,可求得△AEF的周长.
解答:解:在Rt△ABC中,AC=
=10cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
EF=
OD=
BD=
AC=
cm,
AF=
AD=
BC=4cm,AE=
AO=
AC=
,
∴△AEF的周长=AE+AF+EF=9cm.
| AB2+BC2 |
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
EF=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 2 |
AF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
∴△AEF的周长=AE+AF+EF=9cm.
点评:本题主要考查矩形的性质,掌握矩形的对角线相等且互相平分是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,AB是⊙O的一条弦(非直径),作直径CD,使CD⊥AB,则图中有( )对相等的不重叠的弧.
如图,AB是⊙O的一条弦(非直径),作直径CD,使CD⊥AB,则图中有( )对相等的不重叠的弧.| A、2 | B、3 | C、4 | D、5 |
 如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为
如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为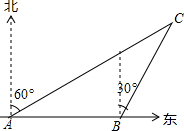 如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?
如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险? 如图所示,△ABC中,中线BD、CE相交于O,F、G分别为OB、OC的中点.判断四边形DEFG的形状并进行证明.
如图所示,△ABC中,中线BD、CE相交于O,F、G分别为OB、OC的中点.判断四边形DEFG的形状并进行证明.