题目内容
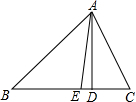 己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC.
己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC.(1)若∠B=50°,∠C=72°,求∠EAD的度数;
(2)若∠B、∠C的度数未知,求证:∠EAD=
| 1 |
| 2 |
考点:三角形内角和定理
专题:计算题
分析:(1)先根据三角形内角和定理可计算出∠BAC=180°-∠B-∠C=58°,再利用角平分线定义得∠CAE=
∠BAC=29°,接着由AD⊥BC得∠ADC=90°,根据三角形内角和得到∠CAD=18°,然后利用∠EAD=∠CAE-∠CAD进行计算;
(2)由三角形内角和定理得∠BAC=180°-∠B-∠C,再根据角平分线定义得∠CAE=
∠BAC=90°-
∠B-
∠C,接着利用互余得到∠CAD=90°-∠C,所以∠EAD=∠CAE-∠CAD=90°-
∠B-
∠C-(90°-∠C),然后整理即可得到结论.
| 1 |
| 2 |
(2)由三角形内角和定理得∠BAC=180°-∠B-∠C,再根据角平分线定义得∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)解:∵∠B=50°,∠C=72°,
∴∠BAC=180°-∠B-∠C=58°,
∵AE平分∠BAC,
∴∠CAE=
∠BAC=29°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-∠C=18°,
∴∠EAD=∠CAE-∠CAD=29°-18°=11°;
(2)证明:∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠CAE=
∠BAC=
(180°-∠B-∠C)=90°-
∠B-
∠C,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-∠C,
∴∠EAD=∠CAE-∠CAD=90°-
∠B-
∠C-(90°-∠C)=
(∠C-∠B).
∴∠BAC=180°-∠B-∠C=58°,
∵AE平分∠BAC,
∴∠CAE=
| 1 |
| 2 |
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-∠C=18°,
∴∠EAD=∠CAE-∠CAD=29°-18°=11°;
(2)证明:∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-∠C,
∴∠EAD=∠CAE-∠CAD=90°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形内角和定理:三角形内角和是180°.注意从特殊到一般,(2)中的结论为一般性结论.

练习册系列答案
相关题目
 如图,A、B两点在函数y=
如图,A、B两点在函数y= 如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为
如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为 在Rt△ABC中,∠C=90°,若AB=4,sinA=
在Rt△ABC中,∠C=90°,若AB=4,sinA=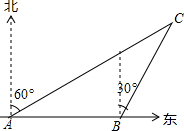 如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?
如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?