题目内容
试计算：三条边长分别为
，
，
的三角形面积．
| 26 |
| 20 |
| 18 |
考点：勾股定理
专题：
分析：根据题意画出图形，进而利用勾股定理求出AD的长，再利用三角形面积公式求出即可．
解答：
解：如图所示：作AD⊥BC于点D，设BD=x，DC=y，
则
，
解得：
，
∴h=
=
，
∴S△ABC=
×
×
=9．
解：如图所示：作AD⊥BC于点D，设BD=x，DC=y，则
|
解得：
|
∴h=
20-
|
| 9 |
| 13 |
| 26 |
∴S△ABC=
| 1 |
| 2 |
| 26 |
| 9 |
| 13 |
| 26 |
点评：此题主要考查了勾股定理，根据题意得出AD的长是解题关键．
练习册系列答案
相关题目
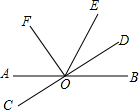如图，直线AB，CD交于O点，OD，OF分别平分∠BOE，∠AOE．
如图，在△ABC中，AB=12，AC=9，D是AC上一点，AD=6，在AB上取一点E，使A，D，E三点组成的三角形与△ABC相似，则AE的长为
在Rt△ABC中，∠C=90°，若AB=4，sinA=