题目内容
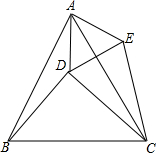 如图,△ABC是等边三角形,△BDC是等腰直角三角形,∠BDC=90°,连接AD,以AD为边作等边△ADE,连接CE.
如图,△ABC是等边三角形,△BDC是等腰直角三角形,∠BDC=90°,连接AD,以AD为边作等边△ADE,连接CE.(1)求证:△CDE为等腰三角形;
(2)求∠AEC的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)证明△ABD≌△ACE,得到BD=CE,结合BD=CD,即可解决问题.
(2)证明△ABD≌△ACD,得到∠BAD=∠CAD=30°;求出∠ABD=15°,运用三角形的内角和定理即可解决问题.
(2)证明△ABD≌△ACD,得到∠BAD=∠CAD=30°;求出∠ABD=15°,运用三角形的内角和定理即可解决问题.
解答: 解:(1)如图,∵△ABC、△ADE均为等边三角形,
解:(1)如图,∵△ABC、△ADE均为等边三角形,
∴∠BAC=∠DAE=60°,AB=AC,AD=AE;
∴∠BAD=∠CAE;
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,而BD=CD,
∴CD=CE,△CDE为等腰三角形.
(2)在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD=30°;
∵△BDC是等腰直角三角形,
∴∠DBC=45°,∠ABD=60°-45°=15°,
∴∠ADB=180°-30°-15°=135°;
∵△ABD≌△ACE,
∴∠AEC=∠ADB=135°.
 解:(1)如图,∵△ABC、△ADE均为等边三角形,
解:(1)如图,∵△ABC、△ADE均为等边三角形,∴∠BAC=∠DAE=60°,AB=AC,AD=AE;
∴∠BAD=∠CAE;
在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE,而BD=CD,
∴CD=CE,△CDE为等腰三角形.
(2)在△ABD与△ACD中,
|
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD=30°;
∵△BDC是等腰直角三角形,
∴∠DBC=45°,∠ABD=60°-45°=15°,
∴∠ADB=180°-30°-15°=135°;
∵△ABD≌△ACE,
∴∠AEC=∠ADB=135°.
点评:该题以等边三角形为载体,以全等三角形的判定及其性质的应用为核心构造而成;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
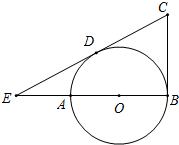 如图,AB是⊙O的直径,BC切⊙O于B,CD切⊙O于D,交AB的延长线于E.若BC=6,EB=8,求EA.
如图,AB是⊙O的直径,BC切⊙O于B,CD切⊙O于D,交AB的延长线于E.若BC=6,EB=8,求EA. 如图,△ABC中,∠A=30°,AC=2
如图,△ABC中,∠A=30°,AC=2 若二次函数y=-x2+bx+c的部分图象如图所示,则关于x的一元二次方程-x2+bx+c=0的一个解是x1=3,则另一个解为
若二次函数y=-x2+bx+c的部分图象如图所示,则关于x的一元二次方程-x2+bx+c=0的一个解是x1=3,则另一个解为 如图,∠B与哪个角是内错角,与哪个角是同旁内角?被哪一条直线所截得形成的?对∠C进行同样的讨论?
如图,∠B与哪个角是内错角,与哪个角是同旁内角?被哪一条直线所截得形成的?对∠C进行同样的讨论? 如图,A、B两点在函数y=
如图,A、B两点在函数y= 如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为
如图,在△ABC中,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使A,D,E三点组成的三角形与△ABC相似,则AE的长为