题目内容
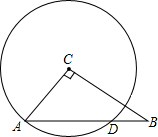 如图,在△ABC中,∠C=90°,AC=9,BC=12,以点C为圆心,AC为半径的圆交AB于点D,求AD的长.
如图,在△ABC中,∠C=90°,AC=9,BC=12,以点C为圆心,AC为半径的圆交AB于点D,求AD的长.考点:垂径定理,勾股定理
专题:
分析:过C作CE⊥AB于E,根据垂径定理得出AD=2AE,根据勾股定理求AB,根据三角形面积公式求出CE,根据勾股定理求出AE即可.
解答: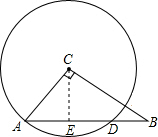 解:过C作CE⊥AB于E,
解:过C作CE⊥AB于E,
∵CE⊥AB,CE过圆心C,
∴AD=2AE.
∵△ABC中,∠C是直角,AC=9,BC=12,
∴由勾股定理得:AB=
=15,
由三角形的面积公式得:AC×BC=AB×CE,即9×12=15CE,
∴CE=
=
,
在△AEC中,由勾股定理得:AE=
=
=
,
∴AD=2AE=
.
 解:过C作CE⊥AB于E,
解:过C作CE⊥AB于E,∵CE⊥AB,CE过圆心C,
∴AD=2AE.
∵△ABC中,∠C是直角,AC=9,BC=12,
∴由勾股定理得:AB=
| AC2+BC2 |
由三角形的面积公式得:AC×BC=AB×CE,即9×12=15CE,
∴CE=
| 9×12 |
| 15 |
| 36 |
| 5 |
在△AEC中,由勾股定理得:AE=
| AC2-CE2 |
92-(
|
| 27 |
| 5 |
∴AD=2AE=
| 54 |
| 5 |
点评:本题考查了勾股定理,垂径定理,三角形的面积等知识点的应用,关键是求出AE的长,主要培养学生运用定理进行推理的能力,题目比较典型,难度适中.

练习册系列答案
相关题目
 在△ABC中,∠ACB=90°,S△BFC:S△AFC=1:3,BC=12,EF⊥BC于点E,求EB的长.
在△ABC中,∠ACB=90°,S△BFC:S△AFC=1:3,BC=12,EF⊥BC于点E,求EB的长. 如图,已知△ABC∽△ACD,AC=6,AD=4,CD=8,求BD,BC的长.
如图,已知△ABC∽△ACD,AC=6,AD=4,CD=8,求BD,BC的长. 直线y=ax+b与直线y=cx+d (a、b、c、d为非零常数)在直角坐标系中的位置如图所示,不等式ax+b<cx+d的解集是
直线y=ax+b与直线y=cx+d (a、b、c、d为非零常数)在直角坐标系中的位置如图所示,不等式ax+b<cx+d的解集是