题目内容
解方程:x2-|x-2|-6=0.
考点:解一元二次方程-公式法
专题:分类讨论
分析:先分两种情况讨论,去掉绝对值,再根据求根公式进行计算即可.
解答:解:x2-|x-2|-6=0,
当x-2>0时,x2-x+2-6=0,
则x2-x-4=0,
解得:x=
=
,
x1=
,x2=
;
当x-2<0时,x2+x-8=0,
解得:x=
=
,
x1=
,x2=
.
当x-2>0时,x2-x+2-6=0,
则x2-x-4=0,
解得:x=
1±
| ||
| 2 |
1±
| ||
| 2 |
x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
当x-2<0时,x2+x-8=0,
解得:x=
-1±
| ||
| 2 |
1±
| ||
| 2 |
x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
点评:此题考查了公式法解一元二次方程,掌握求根公式是本题的关键,注意分两种情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
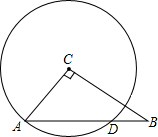 如图,在△ABC中,∠C=90°,AC=9,BC=12,以点C为圆心,AC为半径的圆交AB于点D,求AD的长.
如图,在△ABC中,∠C=90°,AC=9,BC=12,以点C为圆心,AC为半径的圆交AB于点D,求AD的长.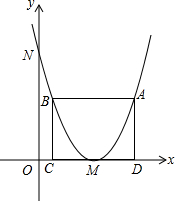 如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4,矩形ABCD的顶点A、B在抛物线上,C、D在x轴上.
如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4,矩形ABCD的顶点A、B在抛物线上,C、D在x轴上.