题目内容
阅读材料:
如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=-
,x1x2=
.
这是一元二次方程根与系数的关系,我们利用它可以用来解题:
设x1,x2是方程x2+6x-3=0的两根,求x
+x
的值.
解法可以这样:∵x1+x2=-6,x1x2=-3,则x
+x
=(x1+x2)2-2x1x2=(-6)2-2×(-3)=42.
请你根据以上解法解答下题:
已知x1,x2是方程x2-4x+2=0的两根,求:
(1)
+
的值;
(2)(x1-x2)2的值;
(3)x12+4x2的值.
如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=-
| b |
| a |
| c |
| a |
这是一元二次方程根与系数的关系,我们利用它可以用来解题:
设x1,x2是方程x2+6x-3=0的两根,求x
| 21 |
| 22 |
解法可以这样:∵x1+x2=-6,x1x2=-3,则x
| 21 |
| 22 |
请你根据以上解法解答下题:
已知x1,x2是方程x2-4x+2=0的两根,求:
(1)
| 1 |
| x1 |
| 1 |
| x2 |
(2)(x1-x2)2的值;
(3)x12+4x2的值.
考点:根与系数的关系
专题:阅读型
分析:根据根与系数的关系得到x1+x2=4,x1x2=2,
(1)先通分得到原式=
,然后利用整体代入的方法计算;
(2)先利用完全平方公式得到原式=(x1+x2)2-4x1x2,然后利用整体代入的方法计算;
(3)先根据一元二次方程得解的定义得到x12=4x1-2,则原式=4(x1+x2)-2,然后利用整体代入的方法计算.
(1)先通分得到原式=
| x1+x2 |
| x1x2 |
(2)先利用完全平方公式得到原式=(x1+x2)2-4x1x2,然后利用整体代入的方法计算;
(3)先根据一元二次方程得解的定义得到x12=4x1-2,则原式=4(x1+x2)-2,然后利用整体代入的方法计算.
解答:解:x1+x2=4,x1x2=2,
(1)原式=
=
=2;
(2)原式=(x1+x2)2-4x1x2=42-4×2=8;
(3)∵x1是方程x2-4x+2=0的根,
∴x12-4x1+2=0,即x12=4x1-2,
∴原式=4x1-2+4x2
=4(x1+x2)-2
=4×4-2
=14.
(1)原式=
| x1+x2 |
| x1x2 |
| 4 |
| 2 |
(2)原式=(x1+x2)2-4x1x2=42-4×2=8;
(3)∵x1是方程x2-4x+2=0的根,
∴x12-4x1+2=0,即x12=4x1-2,
∴原式=4x1-2+4x2
=4(x1+x2)-2
=4×4-2
=14.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了一元二次方程的解.
| b |
| a |
| c |
| a |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
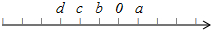 有理数a,b,c,d,在数轴上的位置一条轴,有5个点,距离相等,第一个点表示d,第二个点表示c,第3个点表示b,第4个点表示0,第5个点表示a.
有理数a,b,c,d,在数轴上的位置一条轴,有5个点,距离相等,第一个点表示d,第二个点表示c,第3个点表示b,第4个点表示0,第5个点表示a. 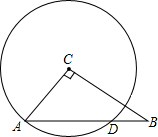 如图,在△ABC中,∠C=90°,AC=9,BC=12,以点C为圆心,AC为半径的圆交AB于点D,求AD的长.
如图,在△ABC中,∠C=90°,AC=9,BC=12,以点C为圆心,AC为半径的圆交AB于点D,求AD的长.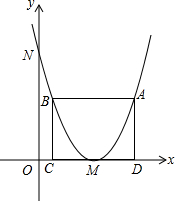 如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4,矩形ABCD的顶点A、B在抛物线上,C、D在x轴上.
如图,抛物线的顶点M在x轴上,抛物线与y轴交于点N,且OM=ON=4,矩形ABCD的顶点A、B在抛物线上,C、D在x轴上.