题目内容
16.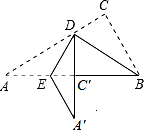 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | 3cm | B. | $2\sqrt{3}$cm | C. | $2\sqrt{5}$cm | D. | $\frac{10}{3}$cm |
分析 根据直角三角形两锐角互余求出∠ABC=60°,翻折前后两个图形能够互相重合可得∠BDC=∠BDC′,∠CBD=∠ABD=30°,∠ADE=∠A′DE,然后求出∠BDE=90°,再解直角三角形求出BD,然后求出DE即可.
解答 解:∵△ABC是直角三角形,∠A=30°,
∴∠ABC=90°-30°=60°,
∵沿折痕BD折叠点C落在斜边上的点C′处,
∴∠BDC=∠BDC′,∠CBD=∠ABD=$\frac{1}{2}$∠ABC=30°,
∵沿DE折叠点A落在DC′的延长线上的点A′处,
∴∠ADE=∠A′DE,
∴∠BDE=∠ABD+∠A′DE=$\frac{1}{2}$×180°=90°,
在Rt△BCD中,BD=BC÷cos30°=5÷$\frac{\sqrt{3}}{2}$=$\frac{10\sqrt{3}}{3}$cm,
在Rt△BDE中,DE=BD•tan30°=$\frac{10\sqrt{3}}{3}$×$\frac{\sqrt{3}}{3}$=$\frac{10}{3}$cm.
故选:D.
点评 本题考查了翻折变换的性质,解直角三角形,熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.如果一个角的两边分别平行于另一个角的两边,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
4.某厂要招聘A,B两个工种的工人共100人,根据工作需要,要求A工种的人数不少B工种人数的$\frac{3}{2}$倍,那么A,B两个工种的月工资如表时,招聘A工种几人才能使这100人每月所付的工资最少?
| 工种 | A | B |
| 月收入(元/人) | 3600 | 1800 |
11.正六边形的边心距是$\sqrt{3}$,则它的边长是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
6.方程$\frac{{x}^{2}-1}{x+1}$=0的解是( )
| A. | 1或-1 | B. | -1 | C. | 0 | D. | 1 |
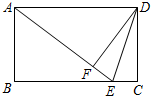 如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=3,BE:EC=4:1,则线段DE的长为$\sqrt{10}$.
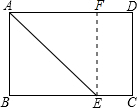 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm. 如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).
如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).