题目内容
5.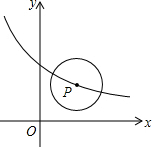 如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).
如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).
分析 根据题意可知,当P点横坐标为±1,或者P点纵坐标为1时,⊙P与坐标轴相切,将横坐标或者纵坐标分别代入y=$\frac{3}{x+2}$中,可求P点坐标.
解答 解:当⊙P与坐标轴相切时,P点的横坐标为±1,或者P点的纵坐标为1,
把x=1代入y=$\frac{3}{x+2}$得:y=1,即此时P点的坐标是(1,1);
把x=-1代入y=$\frac{3}{x+2}$得:y=3,即此时P点的坐标是(-1,3);
把y=1代入y=$\frac{3}{x+2}$得:x=1,即此时P点的坐标是(1,1);
即符合条件的P点的坐标为(1,1)或(-1,3),
故答案为:(1,1)或(-1,3).
点评 本题考查了反比例函数图象上点的坐标特点,圆的切线的判定,还考查了分类讨论的思想.关键是明确圆与坐标轴相切时,圆心与坐标轴的距离等于半径.

练习册系列答案
相关题目
16.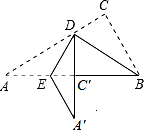 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | 3cm | B. | $2\sqrt{3}$cm | C. | $2\sqrt{5}$cm | D. | $\frac{10}{3}$cm |
13.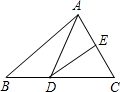 如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
 如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )| A. | 15cm | B. | 18cm | C. | 21cm | D. | 24cm |
15.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
| A. | 若甲对,则乙对 | B. | 若乙对,则甲对 | C. | 若乙错,则甲错 | D. | 若甲错,则乙对 |
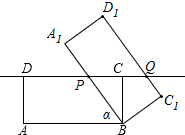 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α≤180)得到矩形A1BC1D1,此时A1B,C1D1这两边所在的直线分别与CD边所在的直线相交于点P、Q,当DP:DQ=1:2时,DP的长为5或1+$\sqrt{11}$.
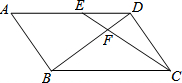 如图,在?ABCD中,点E在AD上,若DE=6,S△DEF:S△BCF=4:25,则AE=9.
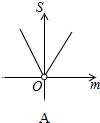
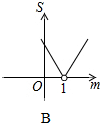
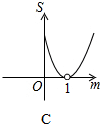
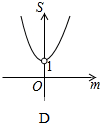
如图,在?ABCD中,点E在AD上,若DE=6,S△DEF:S△BCF=4:25,则AE=9.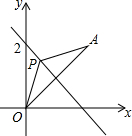 如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )
如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )