题目内容
8.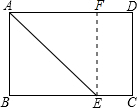 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
分析 根据翻折的性质可得∠B=∠AFE=90°,AB=AF,然后求出四边形ABEF是正方形,再根据正方形的性质可得BE=AB,然后根据CE=BC-BE,代入数据进行计算即可得解.
解答 解:∵沿AE对折点B落在边AD上的点F处,
∴∠B=∠AFE=90°,AB=AF,
又∵∠BAD=90°,
∴四边形ABEF是正方形,
∴BE=AB=6cm,
∴CE=BC-BE=8-6=2cm.
故答案为:2.
点评 本题考查了矩形的性质,正方形的判定与性质,翻折变换的性质,判断出四边形ABEF是正方形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.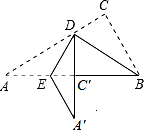 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
 如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )
如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠,使点A落在DC′的延长线上的点A′处.若图中∠C=90°,∠A=30°,BC=5cm,则折痕DE的长为( )| A. | 3cm | B. | $2\sqrt{3}$cm | C. | $2\sqrt{5}$cm | D. | $\frac{10}{3}$cm |
13.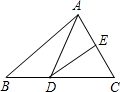 如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
 如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )
如图,△ABC的周长为21cm,将△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=3cm,则△ABD的周长是( )| A. | 15cm | B. | 18cm | C. | 21cm | D. | 24cm |
18.下列说法中正确的是( )
| A. | “打开电视,正在播放新闻节目”是必然事件 | |
| B. | “抛一枚硬币,正面向上的概率为$\frac{1}{2}$”表示每抛两次就有一次正面朝上 | |
| C. | “抛一枚均匀的正方体骰子,朝上的点数是6的概率为$\frac{1}{6}$”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在$\frac{1}{6}$附近 | |
| D. | 为了解某种节能灯的使用寿命,选择全面调查 |
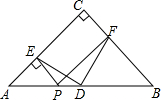 △ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.
△ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.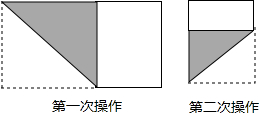
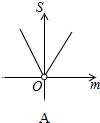
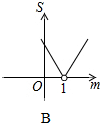
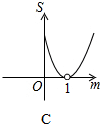
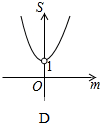
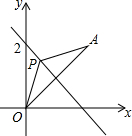 如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )
如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )