题目内容
8.襄阳地区近年来城市发展迅速,交通道路的扩展带动园林绿化的蓬勃发展,襄阳“紫薇公司看到了其中蕴含的商机,经市场调查发现,城市绿化主要需鉴两种不同景观树木.大型造型树木和小型景观乔木.其中大型造型树木和小型景观乔木所投资的金额与市场利涧存在下表所示的函数对应关系.| 大型造型树木 | 小型景观乔木 | ||||
| 投资金额x(万元) | x | 5 | x | 2 | 4 |
| 市场利润y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.4 | 3.2 |
(2)有一农户投资10万元加盟“襄阳紫薇公司”对这两种景观树木进行投资,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润.
分析 (1)直接利用待定系数法分别得出y1和y2的函数解析式;
(2)设投资小型景观乔木x万元,则大型造型树木(10-x)万元,获得利润W万元,列出函数关系式求出最大利润.
解答 解:(1))∵当x=5时,y1=2,
∴2=5k,
∴k=0.4.
∴y1=0.4x.
当x=2时,y2=2.4;
当x=4时,y2=3.2
∴$\left\{\begin{array}{l}{4a+2b=2.4}\\{16a+4b=3.2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.2}\\{b=1.6}\end{array}\right.$.
∴y2=-0.2x2+1.6x.
(2)设小型景观乔木x万元,则大型造型树木(10-x)万元,获得利润W万元,
根据题意可得W=-0.2x2+1.6x+0.4(10-x)=-0.2x2+1.2x+4,
∴W=-0.2(x-3)2+5.8,
当小型景观乔木3万元时,可以获得最大利润5.8万元,
所以大型造型树木7万元,小型景观乔木3万元,这样投资可以获得最大利润5.8万元.
点评 此题主要考查了二次函数的应用,此题难点在第二个问题,求出利润表达式,运用函数性质求最值,常用配方法或公式法.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
18.小丽购买学习用品的收据如下表,因污损导致部分数据无法识别.根据如表,解决下列问题:
(1)小丽此次购买自动铅笔、记号笔各几支?
(2)若小丽计划再次购买自动铅笔、记号笔共10支,且总价不超过30元,则记号笔至多购买多少支?
(1)小丽此次购买自动铅笔、记号笔各几支?
(2)若小丽计划再次购买自动铅笔、记号笔共10支,且总价不超过30元,则记号笔至多购买多少支?
| 商品名 | 单价(元) | 数量(个) | 金额(元) |
| 签字笔 | 3 | 2 | 6 |
| 自动铅笔 | 1.5 | ● | ● |
| 记号笔 | 4 | ● | ● |
| 软皮笔记本 | ● | 2 | 9 |
| 圆规 | 3.5 | 1 | ● |
| 合计 | 8 | 28 |
13.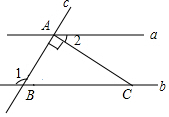 如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )
如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )
 如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )
如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )| A. | 128° | B. | 90° | C. | 52° | D. | 38° |