题目内容
11.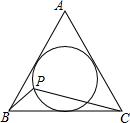 点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.
点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.
分析 设O是△ABC内切圆的圆心,D是切点,连接CD交⊙O于F,CP交⊙O于G,E为CD的中点,连接BE,作EN⊥BC于.首先证明PB+$\frac{1}{2}$PC=PB+PE,当B,P,E共线时,PB+$\frac{1}{2}$PC=PB+PE=BE取最小值,
解答 解:设O是△ABC内切圆的圆心,D是切点,连接CD交⊙O于F,CP交⊙O于G,E为CD的中点,连接BE,作EN⊥BC于.
∵△ABC是等边三角形,
∴CD⊥AB,
∴D是⊙O与AB的切点,O为△ABC的重心,
∴OD=$\frac{1}{3}$CD,
∵CD=BC•cos30°=8$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=12,OD=OF=CF=4,
∴CO=8,CE=6,OG=4,
由切割线定理得,CG•CP=CF•CD=4×12=CO•CE,即$\frac{CG}{CO}=\frac{CE}{CP}$,
∴△ECP∽△GCO,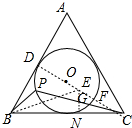
∴$\frac{PE}{PC}=\frac{OG}{OC}$=$\frac{4}{8}$=$\frac{1}{2}$,
∵B,E均为定点,
∴BP+$\frac{1}{2}$PC=BP+PE≤BE,
∴当B,P,E共线时,PB+$\frac{1}{2}$PC=PB+PE=BE取最小值,
在RT△ECN中,∵∠BCE=30°,EC=6,
∴EN=3,CN=3$\sqrt{3}$,BN=5$\sqrt{3}$
∴BE=$\sqrt{E{N}^{2}+B{N}^{2}}$=$\sqrt{{3}^{2}+(5\sqrt{3})^{2}}$=2$\sqrt{21}$,
综上,BP+$\frac{1}{2}$PC的最小值是2$\sqrt{21}$.
故答案为2$\sqrt{21}$.
点评 本题考查了三角形的内切圆与内心,等边三角形的性质,切线的判定和性质,切割线定理,余弦定理,熟练掌握切割线定理,添加辅助线是解题的关键.

| x | -1 | 0 | 1 |
| y | 1 | m | -5 |
| A. | 函数图象必经过点(-2,1) | B. | 函数图象经过第一、二、三象限 | ||
| C. | 函数值y随x的增大而增大 | D. | 当x>$\frac{1}{2}$,时,y<0 |
| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
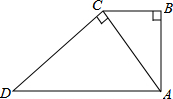 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则△ABC与△DCA的面积比为( )
| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | $\sqrt{2}$:$\sqrt{3}$ |
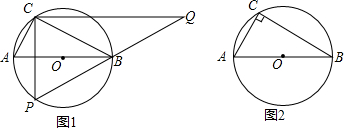 如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.
如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.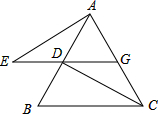 已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.
已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.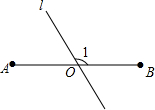 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.