题目内容
17.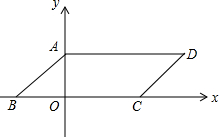 如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(-4,0)
如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(-4,0)(1)求点D的坐标;
(2)设点P是边BC上(不与点B、C重合)的一个动点,设点P的坐标为(m,0),△ABP的面积为s,求△ABP的面积s关于m的函数关系式,并写出自变量m的取值范围;
(3)直接写出当△ABP为等腰三角形时点P的坐标.
分析 (1)根据勾股定理求出OA,根据平行四边形的性质求出点D的坐标;
(2)分点P在OB上和点P在OC上两种情况,根据三角形的面积公式计算即可;
(3)分AB=AP、AB=BP、AP=BP三种情况,根据等腰三角形的性质、勾股定理解答.
解答 解:(1)∵点B的坐标为(-4,0)
∴OB=4,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=3,
∴点D的坐标为(10,3);
(2)当点P在OB上时,s=$\frac{1}{2}$×(4-m)×3=-$\frac{3}{2}$m+6,
当点P在OC上时,s=$\frac{1}{2}$×(4+m)×3=$\frac{3}{2}$m+6,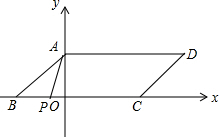
则s关于m的函数关系式s=$\left\{\begin{array}{l}{-\frac{3}{2}m+6(-4<m<0)}\\{\frac{3}{2}m+6(0<m<6)}\end{array}\right.$;
(3)当AB=AP时,OP=OB=4,
则点P的坐标为(4,0),
当AB=BP=5时,OP=BP-OB=1,
则点P的坐标为(1,0),
如图,当AP=BP时,BP=AP=OB-OP=4-OP,
由勾股定理得,OP2+OA2=AP2,即(4-OP)2=32+OP2,
解得,OP=$\frac{7}{8}$,
则点P的坐标为(-$\frac{7}{8}$,0),
综上所述,当△ABP为等腰三角形时点P的坐标为(4,0)或(1,0)或(-$\frac{7}{8}$,0).
点评 本题考查的是平行四边形的性质、一次函数解析式的确定、勾股定理的应用,掌握平行四边形的性质、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
8.2017的倒数是( )
| A. | $\frac{1}{2017}$ | B. | -2017 | C. | 2017 | D. | $\sqrt{2017}$ |
7. 如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
 如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
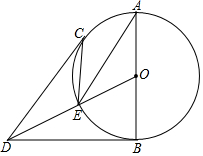 如图,AB是⊙O的直径,DB,DC分别与⊙O相切于B,C,OD交⊙O于点E,
如图,AB是⊙O的直径,DB,DC分别与⊙O相切于B,C,OD交⊙O于点E, 已知:如图,四边形ABCD中,DB⊥BC,DB平分∠ADC,点E为边CD的中点,AB⊥BE.
已知:如图,四边形ABCD中,DB⊥BC,DB平分∠ADC,点E为边CD的中点,AB⊥BE.