题目内容
9.某工厂从外地用4万元和1.44万元分别购买A、B两种原料,若A种原料的进价每吨比B种原料多800元,且购得A种原料比B种原料多$\frac{2}{3}$,现计划租用甲、乙两种货车共8辆将购得的两种原料一次性运回工厂.(1)购得A、B两种原料各是多少吨?
(2)设安排甲种货车y辆.
①已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A、B两种原料各2吨.如何安排甲、乙两种货车?写出所有可行方案.
②若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元,总运费为W元,求W(元)与(y辆)之间的函数关系式:在①的前提下,y为何值时,总运费W最小?最小值是多少元?
分析 (1)根据题意可以得到相应的方程组,从而可以解答本题;
(2)①根据题意可以得到相应的不等式组,从而可以解答本题;
②根据题意可以得到W关于y的函数关系式,由①中的方案和函数关系式即可解答本题.
解答 解:(1)设购买A种原料x吨,B种原料y吨,
$\left\{\begin{array}{l}{\frac{40000}{x}-\frac{14400}{y}=800}\\{x=y+\frac{2}{3}y}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=20}\\{y=12}\end{array}\right.$,
即A、B两种原料各是20吨、12吨;
(2)①由题意可得,
$\left\{\begin{array}{l}{4y+2(8-y)≥20}\\{y+2(8-y)≥12}\end{array}\right.$,
解得,2≤y≤4,
∴可行的方案有三种,
方案一:甲种货车2辆,乙种货车6辆;
方案二:甲种货车3辆,乙种货车5辆;
方案三:甲种货车4辆,乙种货车4辆;
②由题意可得,
W(元)与(y辆)之间的函数关系式为:W=400y+350(8-y)=50y+2800,
∴方案一:甲种货车2辆,乙种货车6辆所用的费用最少,此时的费用为:50×2+2800=2900(元),
即W(元)与(y辆)之间的函数关系式为:W=50y+2800,方案一:甲种货车2辆,乙种货车6辆所用的总费用W最小,最小值为2900元.
点评 本题考查一次函数的应用、不等式的应用、解方程组,解答本题的关键是明确题意,求出相应的函数关系式,列出相应的方程,利用不等式的性质和一次函数的性质解答.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.计算(x+2)2,正确的是( )
| A. | x2+4 | B. | x2+2 | C. | x2+4x+4 | D. | 2x+4 |
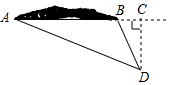 钓鱼岛是我国固有领土,东西长约3641米,如图所示,某海警船巡航到点D处时,测得岛上最东端“东钓角”(A点处)的方向角为北偏西67.5°,最西端“西钓角”(B点处)的方向角为北偏西30°,已知此时海警船到直线AB的距离是2000米,根据以上数据,请求出钓鱼岛东西长度AB的距离,并比较你的计算结果与实际长度的误差(参考数据:tan30°≈0.578,tan67.5°≈2.414,cos30°≈1.732,cot67.5°≈0.414)
钓鱼岛是我国固有领土,东西长约3641米,如图所示,某海警船巡航到点D处时,测得岛上最东端“东钓角”(A点处)的方向角为北偏西67.5°,最西端“西钓角”(B点处)的方向角为北偏西30°,已知此时海警船到直线AB的距离是2000米,根据以上数据,请求出钓鱼岛东西长度AB的距离,并比较你的计算结果与实际长度的误差(参考数据:tan30°≈0.578,tan67.5°≈2.414,cos30°≈1.732,cot67.5°≈0.414)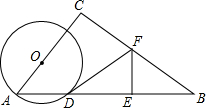 如图,在Rt△ABC中,∠C=90°,tanA=$\frac{4}{3}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连接DF.
如图,在Rt△ABC中,∠C=90°,tanA=$\frac{4}{3}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连接DF.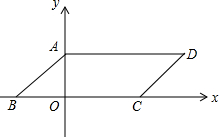 如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(-4,0)
如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(-4,0)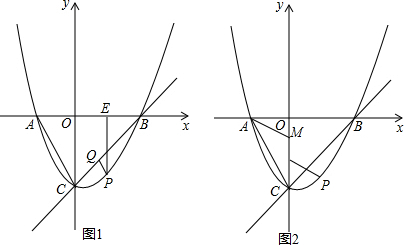
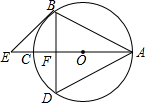 如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点
如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点