题目内容
2．已知方程x2-2x+tanA=0只有一个解，求锐角A的度数．分析 根据方程只有一个实数根结合根的判别式即可得出△=4-4tanA=0，解之即可得出tanA的值，再由∠A为锐角即可得出结论．
解答 解：∵方程x2-2x+tanA=0只有一个解，
∴△=（-2）2-4tanA=4-4tanA=0，
解得：tanA=1，
∴锐角A的度数为45°．
点评 本题考查了根的判别式以及特殊角的三角函数值，熟练掌握“当△=0时，方程有两个相等的实数根”是解题的关键．
练习册系列答案
相关题目
12．AD是△ABC的高，AC=2$\sqrt{5}$，AD=4，把△ADC沿着直线AD对折，点C落在点E的位置，如果△ABE是等腰三角形，那么线段BE的长度为（ ）
| A． | 2$\sqrt{5}$ | B． | 2$\sqrt{5}$或5 | C． | 2$\sqrt{6}$ | D． | 5 |
13．化简$\frac{1}{a-2}$-$\frac{2a}{{a}^{2}-4}$的结果等于为（ ）
| A． | -a-2 | B． | -$\frac{1}{a+2}$ | C． | $\frac{1}{a+2}$ | D． | $\frac{1}{a-2}$ |
10．
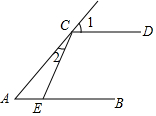如图，AB∥CD，CE于AB交于E点，∠1=50°，∠2=15°，则∠CEB的度数为（ ）
如图，AB∥CD，CE于AB交于E点，∠1=50°，∠2=15°，则∠CEB的度数为（ ）| A． | 50° | B． | 60° | C． | 65° | D． | 70° |
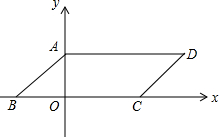如图，四边形ABCD是平行四边形，AB=5，BC=10，顶点A在y轴上，边BC在x轴上，且点B的坐标为（-4，0）
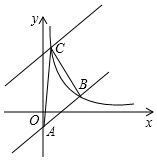如图，在平面直角坐标系xOy中，直线y=x-2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）
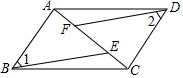四边形ABCD是平行四边形，AF=CE，求证：∠1=∠2．