题目内容
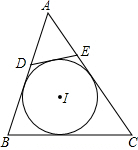如图，⊙I为△ABC的内切圆，点D，E分别为边AB，AC上的点，且DE为⊙I的切线，若△ABC的周长为20，BC边的长为6，则△ADE的周长为考点：三角形的内切圆与内心
专题：
分析：利用切线长定理可得BF=BG，DG=DI，EH=EI，CF=CH，据此即可求解．
解答：
解：∵BG和BF是圆的切线，
∴BF=BG，
同理，DG=DI，EH=EI，CF=CH．
∴BG+CH=BC=6，
△ADE的周长=AD+AE+DE=AD+AE+DI+IE=AD+AE+DG+EH=AG+AH=20-6-6=8．
故答案是：8．
解：∵BG和BF是圆的切线，∴BF=BG，
同理，DG=DI，EH=EI，CF=CH．
∴BG+CH=BC=6，
△ADE的周长=AD+AE+DE=AD+AE+DI+IE=AD+AE+DG+EH=AG+AH=20-6-6=8．
故答案是：8．
点评：本题考查了切线长定理，正确求得BG+CH的长是关键．
练习册系列答案
相关题目
如图，正方形ABCD的边长为6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．则下列结论：①△ABG≌△AFG；②BG=CG；③AG∥CF；④S△EGC=S△AFE；⑤∠AGB+∠AED=135°．其中正确的个数是（ ）