题目内容
在△ABC中,AB=26,AC=25,高AD=24.
(1)求三角形外接圆的半径;
(2)直接写出能覆盖△ABC的最小圆的半径.
(1)求三角形外接圆的半径;
(2)直接写出能覆盖△ABC的最小圆的半径.
考点:三角形的外接圆与外心
专题:计算题
分析:(1)作直径CE,连接AE,如图,根据圆周角定理得∠CEA=90°,∠B=∠E,则可证明Rt△AEC∽Rt△DBA,利用相似比可计算出CE=
,则半径OE=
;
(2)根据三角形外接圆的定义,能覆盖△ABC的最小圆就是它的外接圆,所以能覆盖△ABC的最小圆的半径为
.
| 325 |
| 12 |
| 325 |
| 24 |
(2)根据三角形外接圆的定义,能覆盖△ABC的最小圆就是它的外接圆,所以能覆盖△ABC的最小圆的半径为
| 325 |
| 24 |
解答:解:(1) ⊙O为△ABC的外接圆,作直径CE,连接AE,如图,
⊙O为△ABC的外接圆,作直径CE,连接AE,如图,
∵AD为△ABC的高,
∴∠ADB=90°,
∵CE为直径,
∴∠CEA=90°,
∵∠B=∠E,
∴Rt△AEC∽Rt△DBA,
∴CE:AB=AC:AD,即CE:26=25:24,
∴CE=
,
∴OE=
,
即三角形外接圆的半径为
;
(2)能覆盖△ABC的最小圆的半径为
.
 ⊙O为△ABC的外接圆,作直径CE,连接AE,如图,
⊙O为△ABC的外接圆,作直径CE,连接AE,如图,∵AD为△ABC的高,
∴∠ADB=90°,
∵CE为直径,
∴∠CEA=90°,
∵∠B=∠E,
∴Rt△AEC∽Rt△DBA,
∴CE:AB=AC:AD,即CE:26=25:24,
∴CE=
| 325 |
| 12 |
∴OE=
| 325 |
| 24 |
即三角形外接圆的半径为
| 325 |
| 24 |
(2)能覆盖△ABC的最小圆的半径为
| 325 |
| 24 |
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆;三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和相似三角形的判定与性质.

练习册系列答案
相关题目
近似数7.8×104是精确到( )的近似数.
| A、十分位 | B、百位 | C、千位 | D、万位 |
 如图,已知线段a、b、m,
如图,已知线段a、b、m,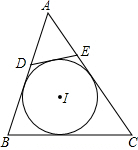 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为