题目内容
 如图,正方形ABCD的边长为6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=135°.其中正确的个数是( )
如图,正方形ABCD的边长为6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=135°.其中正确的个数是( )| A、5 | B、4 | C、3 | D、2 |
考点:全等三角形的判定与性质
专题:
分析:结合条件可证明Rt△ABG≌Rt△AFG,在Rt△EGC中由勾股定理可求得BG=CG=3,BG+CG=6,满足条件,利用外角的性质可求得∠AGB=∠GCF,可得AG∥CF,可求得S△EGC=S△AFE=6,利用多边形的内角和可求得2∠AGB+2∠AED=270°,可得∠AGB+∠AED=135°,所以五个结论都正确.
解答:解:由题意可求得DE=2,CE=4,AB=BC=AD=6,
∵将△ADE沿AE对折至△AFE,
∴∠AFE=∠ADE=∠ABG=90°,AF=AD=AB,EF=DE=2
在Rt△ABG和Rt△AFG中
,
∴Rt△ABG≌Rt△AFG(HL),
∴①正确;
∴BG=GF,∠BGA=∠FGA,
设BG=GF=x,若BG=CG=x,在Rt△EGC中,EG=x+2,CG=x,CE=4,由勾股定理可得(x+2)2=x2+42,
解得x=3,此时BG=CG=3,BG+CG=6,满足条件,
∴②正确;
∵GC=GF,
∴∠GFC=∠GCF,
且∠BGF=∠GFC+∠GCF=2∠GCF,
∴2∠AGB=2∠GCF,
∴∠AGB=∠GCF,
∴AG∥CF,
∴③正确;
∵S△EGC=
GC•CE=
×3×4=6,S△AFE=
AF•EF=
×6×2=6,
∴S△EGC=S△AFE,
∴④正确;
在五边形ABGED中,
∠BGE+∠GED=540°-90°-90°-90°=270°,
即2∠AGB+2∠AED=270°,
∴∠AGB+∠AED=135°,
∴⑤正确;
∴正确的有五个,
故选A.
∵将△ADE沿AE对折至△AFE,
∴∠AFE=∠ADE=∠ABG=90°,AF=AD=AB,EF=DE=2
在Rt△ABG和Rt△AFG中
|
∴Rt△ABG≌Rt△AFG(HL),
∴①正确;
∴BG=GF,∠BGA=∠FGA,
设BG=GF=x,若BG=CG=x,在Rt△EGC中,EG=x+2,CG=x,CE=4,由勾股定理可得(x+2)2=x2+42,
解得x=3,此时BG=CG=3,BG+CG=6,满足条件,
∴②正确;
∵GC=GF,
∴∠GFC=∠GCF,
且∠BGF=∠GFC+∠GCF=2∠GCF,
∴2∠AGB=2∠GCF,
∴∠AGB=∠GCF,
∴AG∥CF,
∴③正确;
∵S△EGC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△EGC=S△AFE,
∴④正确;
在五边形ABGED中,
∠BGE+∠GED=540°-90°-90°-90°=270°,
即2∠AGB+2∠AED=270°,
∴∠AGB+∠AED=135°,
∴⑤正确;
∴正确的有五个,
故选A.
点评:本题主要考查正方形的性质及全等三角形的判定和性质,利用折叠得到线段相等及角相等、结合多边形内角和及外角性质的运用是解题的关键.

练习册系列答案
相关题目
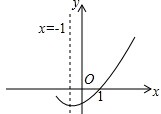 已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )
已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )| A、a+b+c=0 |
| B、b>2a |
| C、ax2+bx+c=0两根是-3和1 |
| D、a-2b+c>0 |
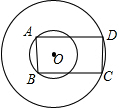 如图所示:两个同心圆,半径分别是2
如图所示:两个同心圆,半径分别是2| 6 |
| 3 |
A、22+6
| ||
B、20+8
| ||
C、18+10
| ||
D、16+12
|
 实数a、b在数轴上的位置如图所示,下列各式中成立的是( )
实数a、b在数轴上的位置如图所示,下列各式中成立的是( )| A、a+b>0 |
| B、ab>0 |
| C、a-b>0 |
| D、|a|>|b| |
在多项式x3-xy2+25中,最高次项是( )
| A、x3 |
| B、x3,xy2 |
| C、x3,-xy2 |
| D、25 |

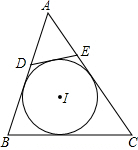 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为