题目内容
奇奇妈妈买了一块正方形地毯,地毯上有“※”组成的图案,观察局部有如此规律:奇奇数※个数的方法是用“L”来划分,从右上角的1个开始,一层一层往外数,第一层1个,第二层3个,第三层5个…,这样她发现了连续奇数求和的方法.
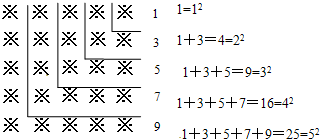
通过阅读上段材料,请完成下列问题:
(1)1+3+5+7+9+…+27+29= .
(2)13+15+17+…+97+99= .
(3)0到200之间,所有能被3整除的奇数的和为 .
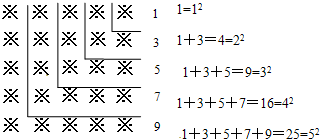
通过阅读上段材料,请完成下列问题:
(1)1+3+5+7+9+…+27+29=
(2)13+15+17+…+97+99=
(3)0到200之间,所有能被3整除的奇数的和为
考点:规律型:数字的变化类,有理数的加法
专题:
分析:(1)观察不难发现,从1开始的连续奇数的和等于首尾两个计算的和的一半的平方,然后计算即可得解;
(2)用从1开始到99的奇数的和减去从1开始到11的奇数的和,列式计算即可得解;
(3)根据题意列式算式,然后提取3,再利用(1)的计算方法进行计算即可得解.
(2)用从1开始到99的奇数的和减去从1开始到11的奇数的和,列式计算即可得解;
(3)根据题意列式算式,然后提取3,再利用(1)的计算方法进行计算即可得解.
解答:解:(1)1+3+5+7+9+…+27+29=(
)2=225;
(2)13+15+17+…+97+99=(
)2-(
)2=2500-36=2464;
(3)由题意得,所有奇数的和=3+3×3+3×5+…+3×65,
=3×(1+3+5+…+65),
=3×(
)2,
=3×1089,
=3267.
故答案为:(1)225;(2)2464;(3)3267.
| 1+29 |
| 2 |
(2)13+15+17+…+97+99=(
| 1+99 |
| 2 |
| 1+11 |
| 2 |
(3)由题意得,所有奇数的和=3+3×3+3×5+…+3×65,
=3×(1+3+5+…+65),
=3×(
| 1+65 |
| 2 |
=3×1089,
=3267.
故答案为:(1)225;(2)2464;(3)3267.
点评:本题是对数字变化规律的考查,观察出从1开始的连续奇数的和等于首尾两个计算的和的一半的平方是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中,错误的是( )
| A、实数与数轴上的点一一对应 |
| B、数轴上的点表示的数若不是有理数就是无理数 |
| C、有理数的运算及性质,在实数运算中仍成立 |
| D、对于实数a,若|a|=a,则a>0 |
 实数a、b在数轴上的位置如图所示,下列各式中成立的是( )
实数a、b在数轴上的位置如图所示,下列各式中成立的是( )| A、a+b>0 |
| B、ab>0 |
| C、a-b>0 |
| D、|a|>|b| |
 如图所示,在直角坐标系中,直线AB:y=-
如图所示,在直角坐标系中,直线AB:y=-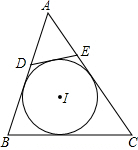 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为 如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=7,AC=5,则BD的长为
如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=7,AC=5,则BD的长为