题目内容
直角三角形的两条直角边长分别为6和8,那么这个三角形的内切圆半径等于 .
考点:三角形的内切圆与内心
专题:计算题
分析:如图,△ABC为直角三角形,∠C=90°,AC=8,BC=6,⊙O为△ABC的内切圆,与各边的切点分别为D、E、F,连接OD、OE、OF,设⊙O的半径为r,
先利用勾股定理计算出AB=10,根据切线的性质得OD=OE=r,OD⊥AC,OE⊥BC,再证明四边形ODCE为正方形,得到CD=CE=OE=r,则AD=8-r,BE=6-r,
然后根据切线长定理得到AF=AD=8-r,BF=BE=6-r,于是有8-r+6-r=10,然后解方程即可得到r的值.
先利用勾股定理计算出AB=10,根据切线的性质得OD=OE=r,OD⊥AC,OE⊥BC,再证明四边形ODCE为正方形,得到CD=CE=OE=r,则AD=8-r,BE=6-r,
然后根据切线长定理得到AF=AD=8-r,BF=BE=6-r,于是有8-r+6-r=10,然后解方程即可得到r的值.
解答:解:如图,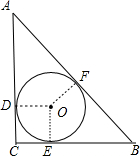 △ABC为直角三角形,∠C=90°,AC=8,BC=6,⊙O为△ABC的内切圆,与各边的切点分别为D、E、F,
△ABC为直角三角形,∠C=90°,AC=8,BC=6,⊙O为△ABC的内切圆,与各边的切点分别为D、E、F,
连接OD、OE、OF,设⊙O的半径为r,
在Rt△ABC中,AB=
=10,
则OD=OE=r,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为矩形,
而OD=OE,
∴四边形ODCE为正方形,
∴CD=CE=OE=r,
∴AD=8-r,BE=6-r,
∵AF=AD=8-r,BF=BE=6-r,
∴8-r+6-r=10,解得r=2,
即这个三角形的内切圆半径等于2.
故答案为2.
 △ABC为直角三角形,∠C=90°,AC=8,BC=6,⊙O为△ABC的内切圆,与各边的切点分别为D、E、F,
△ABC为直角三角形,∠C=90°,AC=8,BC=6,⊙O为△ABC的内切圆,与各边的切点分别为D、E、F,连接OD、OE、OF,设⊙O的半径为r,
在Rt△ABC中,AB=
| AC2+BC2 |
则OD=OE=r,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为矩形,
而OD=OE,
∴四边形ODCE为正方形,
∴CD=CE=OE=r,
∴AD=8-r,BE=6-r,
∵AF=AD=8-r,BF=BE=6-r,
∴8-r+6-r=10,解得r=2,
即这个三角形的内切圆半径等于2.
故答案为2.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.也考查了切线的性质与切线长定理;记住直角边为a、b,斜边为c的三角形内切圆半径等于
.
| a+b-c |
| 2 |

练习册系列答案
相关题目
 如图,已知线段a、b、m,
如图,已知线段a、b、m,
 如图所示,在直角坐标系中,直线AB:y=-
如图所示,在直角坐标系中,直线AB:y=-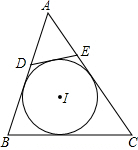 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为 如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=7,AC=5,则BD的长为
如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=7,AC=5,则BD的长为