题目内容
?ABCD中,点E、F分别在DC、DA上,且AE=CF,AE、CF相交于点O,求证:OB平分∠AOC.
考点:平行四边形的性质
专题:证明题
分析:首先连接BE、BF,作BM⊥AE,BN⊥CF,进而利用三角形面积公式以及平行四边形的性质得出BM=BN,即可得出答案.
解答: 证明:连接BE、BF,作BM⊥AE,BN⊥CF,
证明:连接BE、BF,作BM⊥AE,BN⊥CF,
∵四边形ABCD是平行四边形,
∴S△ABE=S△BCF=
S平行四边形ABCD,
∵S△ABE=
BM×AE,
S△BCF=
BN×CF,且AE=CF,
∴BM=BN,根据到角的两边距离相等的点在这个角平分线上,
∴点B在∠AOC的平分线上,即BO∠平分∠AOC.
 证明:连接BE、BF,作BM⊥AE,BN⊥CF,
证明:连接BE、BF,作BM⊥AE,BN⊥CF,∵四边形ABCD是平行四边形,
∴S△ABE=S△BCF=
| 1 |
| 2 |
∵S△ABE=
| 1 |
| 2 |
S△BCF=
| 1 |
| 2 |
∴BM=BN,根据到角的两边距离相等的点在这个角平分线上,
∴点B在∠AOC的平分线上,即BO∠平分∠AOC.
点评:此题主要考查了平行四边形的性质和角平分线的判定等知识,得出BN=BM是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
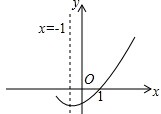 已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )
已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )| A、a+b+c=0 |
| B、b>2a |
| C、ax2+bx+c=0两根是-3和1 |
| D、a-2b+c>0 |
 实数a、b在数轴上的位置如图所示,下列各式中成立的是( )
实数a、b在数轴上的位置如图所示,下列各式中成立的是( )| A、a+b>0 |
| B、ab>0 |
| C、a-b>0 |
| D、|a|>|b| |
 如图,已知线段a、b、m,
如图,已知线段a、b、m,
 如图所示,在直角坐标系中,直线AB:y=-
如图所示,在直角坐标系中,直线AB:y=-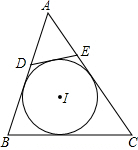 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为 如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积是49.若点A对应的数是-2,则点B对应的数是( )
如图,点A,B在数轴上,以AB为边作正方形,该正方形的面积是49.若点A对应的数是-2,则点B对应的数是( )