题目内容
求两条直角边分别为8、15的直角三角形斜边上的高.
考点:勾股定理
专题:
分析:根据勾股定理求出AB,根据三角形的面积公式求出即可.
解答:
解:在Rt△ACB中,由勾股定理得:AB=
=
=17,
根据三角形的面积公式得:
AC×BC=
×AB×CD,
8×15=17×CD,
解得:CD=
,
即两条直角边分别为8、15的直角三角形斜边上的高是
.

解:在Rt△ACB中,由勾股定理得:AB=
| AC2+BC2 |
| 152+82 |
根据三角形的面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
8×15=17×CD,
解得:CD=
| 120 |
| 17 |
即两条直角边分别为8、15的直角三角形斜边上的高是
| 120 |
| 17 |
点评:本题考查了勾股定理和三角形的面积公式的应用,解此题的关键是求出斜边AB的长和根据三角形的面积得出AB×CD=AC×BC.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
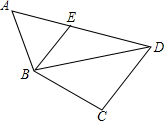 如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )
如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )| A、75° | B、65° |
| C、63° | D、61° |
下列说法中,不正确的是( )
| A、8的立方根是2 |
| B、-8的立方根是-2 |
| C、0的立方根是0 |
| D、-1的立方根是1 |
下列各式计算正确的是( )
| A、2a+2=3a2 |
| B、(-b3)2=-b6 |
| C、c2•c3=c5 |
| D、(m-n)2=m2-n2 |
对角线互相垂直平分的四边形一定是( )
| A、梯形 | B、菱形 | C、矩形 | D、正方形 |