题目内容
已知不等式-x+5>3x-3的解集是2<x,则直线y=-x+5与y=3x-3的交点坐标是( )
| A、(2,3) |
| B、(3,2) |
| C、(3,-2) |
| D、(-3,2) |
考点:一次函数与一元一次不等式
专题:计算题
分析:根据一次函数与一元一次不等式的关系得到直线y=-x+5与y=3x-3的交点的横坐标为2,然后利用一次函数图象上点的坐标特征求出对应的纵坐标即可.
解答:解:∵不等式-x+5>3x-3的解集是2<x,
∴直线y=-x+5与y=3x-3的交点的横坐标为2,
而x=2时,y=-x+5=3,
∴直线y=-x+5与y=3x-3的交点坐标为(2,3).
故选A.
∴直线y=-x+5与y=3x-3的交点的横坐标为2,
而x=2时,y=-x+5=3,
∴直线y=-x+5与y=3x-3的交点坐标为(2,3).
故选A.
点评:本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
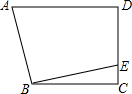 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )| A、6 | B、8 | C、10 | D、无法确定 |
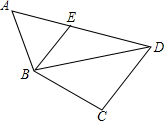 如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )
如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )| A、75° | B、65° |
| C、63° | D、61° |
 如图,在某海岛的观察所A测得船只B的俯角是30°.若观察所的标高(当水位为0m时的高度)是53m,当时的水位是+3m,则观察所A和船只B的水平距离BC是( )
如图,在某海岛的观察所A测得船只B的俯角是30°.若观察所的标高(当水位为0m时的高度)是53m,当时的水位是+3m,则观察所A和船只B的水平距离BC是( )| A、50m | ||
B、50
| ||
| C、5m | ||
D、53
|
对角线互相垂直平分的四边形一定是( )
| A、梯形 | B、菱形 | C、矩形 | D、正方形 |
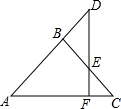 如图,△ABC,AB=BC,DF⊥AC于F,交AB的延长线于D,求证:△DBE是等腰三角形.
如图,△ABC,AB=BC,DF⊥AC于F,交AB的延长线于D,求证:△DBE是等腰三角形.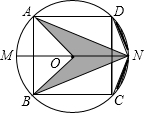 如图所示,正方形ABCD内接于⊙O,直径MN∥AD,则阴影部分面积占圆面积的
如图所示,正方形ABCD内接于⊙O,直径MN∥AD,则阴影部分面积占圆面积的