题目内容
4.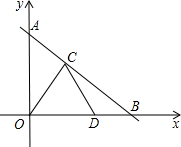 如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.
如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.(1)求B、C两点的坐标;
(2)求直线AB的解析式.
分析 (1)作CH⊥OD于H,如图,根据等边三角形的性质得OH=DH=$\frac{1}{2}$OD=1,再根据勾股定理计算出CH=$\sqrt{3}$,则可得到C点坐标为(1,$\sqrt{3}$);然后利用OD=2DB得到DB=1,则可得到B点坐标为(3,0);
(2)把C(1,$\sqrt{3}$),B(3,0)代入y=kx+b得到关于k、b的方程组,然后解方程组即可.
解答 解:(1)作CH⊥OD于H,如图,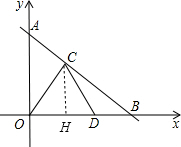 ∵△OCD为等边三角形,
∵△OCD为等边三角形,
∴OH=DH=$\frac{1}{2}$OD=1,
在Rt△OCH中,∵OC=2,OH=1,
∴CH=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴C点坐标为(1,$\sqrt{3}$);
∵OD=2DB,
∴DB=1,
∴OB=3,
∴B点坐标为(3,0);
(2)把C(1,$\sqrt{3}$),B(3,0)代入y=kx+b得$\left\{\begin{array}{l}{k+b=\sqrt{3}}\\{3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{2}}\\{b=\frac{3\sqrt{3}}{2}}\end{array}\right.$.
故直线AB的解析式为y=-$\frac{\sqrt{3}}{2}$x+$\frac{3\sqrt{3}}{2}$.
点评 本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了等边三角形的性质.

练习册系列答案
相关题目
15.数据-3,-2,1,3,6,x的中位数是1,那么这组数据的众数是( )
| A. | 2 | B. | 1 | C. | 1.5 | D. | -2 |
16.直线y=-2x-4与两坐标轴围成的三角形面积是( )
| A. | 3 | B. | 4 | C. | 12 | D. | 6 |
14.若方程3x+2a=12和方程2x-4=12的解相同,则a的值为( )
| A. | 6 | B. | 8 | C. | -6 | D. | 4 |
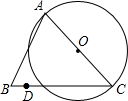 如图,等边三角形ABC的边长为10,以AC为直径作⊙O,D是BC边上一点,BD=2,以D为圆心,DB为半径的⊙D与⊙O的位置关系为外切.
如图,等边三角形ABC的边长为10,以AC为直径作⊙O,D是BC边上一点,BD=2,以D为圆心,DB为半径的⊙D与⊙O的位置关系为外切.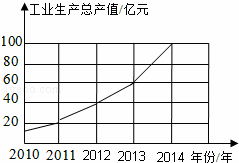 如图是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图可得:增长幅度最大的年份是2014年,比它的前一年增加40亿元.
如图是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图可得:增长幅度最大的年份是2014年,比它的前一年增加40亿元.