Question

12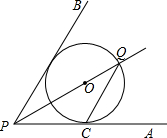．如图，点O在∠APB的平分线上，⊙O与PA相切于点C．
（1）求证：直线PB也与⊙O相切；
（2）PO的延长线与⊙O交于点Q，若⊙O的半径为3，PC=4，求PQ的长．

Answer 1

分析 （1）过点O作OD⊥PB于点D，连接OC，证明OD=OC即可；
（2）过点C作CH⊥OP，利用勾股定理求出OP的值，即得到PQ的值．

解答 （1）证明：过点O作OD⊥PB于点D，连接OC，
∵PA切⊙O于点C，
∴OC⊥PA，
又∵点O在∠APB的角平分线上，
∴OC=OD，即OD的长等于⊙O的半径，
∴PB与⊙O相切；

（2）解：过点C作CH⊥OP于点H，
在Rt△PCO中，PC=4，OC=3，
∴OP=$\sqrt{{OC}^{2}{+PC}^{2}}$=5，
∴PQ=OP+OQ=8．

点评 本题考查了切线的判定方法和勾股定理的运用，作出正确的辅助线是解题的关键．