题目内容
17.若实数m满足m2-$\sqrt{10}$m+1=0,则(m-$\frac{1}{m}$)2=6.分析 已知等式两边除以m变形求出m+$\frac{1}{m}$的值,两边平方并利用完全平方公式化简求出m2+$\frac{1}{{m}^{2}}$的值,原式利用完全平方公式变形,将各自的值代入计算即可求出值.
解答 解:m2-$\sqrt{10}$m+1=0,
变形得:m+$\frac{1}{m}$=$\sqrt{10}$,
两边平方得:(m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$+2=10,即m2+$\frac{1}{{m}^{2}}$=8,
则(m-$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$-2=8-2=6.
故答案为:6
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.在不透明的袋子中有四张标着数字1,2,3,4的卡片.
(1)随机地抽取一张,求P(偶数);
(2)随机地抽取两张,两数字之和是偶数的小明获胜、两数字之和为奇数的小华胜,你认为谁获胜的可能性大?为什么?
(1)随机地抽取一张,求P(偶数);
(2)随机地抽取两张,两数字之和是偶数的小明获胜、两数字之和为奇数的小华胜,你认为谁获胜的可能性大?为什么?
7.两个相似三角形对应中线的比2:3,周长的和是20,则两个三角形的周长分别为( )
| A. | 8和12 | B. | 9和11 | C. | 7和13 | D. | 6和14 |
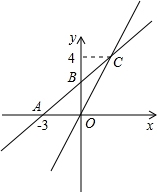 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=$\frac{4}{3}$x的图象交点为C(m,4).求:
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=$\frac{4}{3}$x的图象交点为C(m,4).求: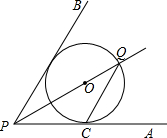 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
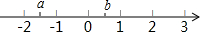 我们可以计算出
我们可以计算出