题目内容
 如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BC=12,∠ABC=60°,则梯形ABCD的周长为
如图,在梯形ABCD中,AD∥BC,AB=AD=CD,BC=12,∠ABC=60°,则梯形ABCD的周长为考点:等腰梯形的性质
专题:
分析:首先过点A作AE∥BC于点E,由在梯形ABCD中,AD∥BC,AB=AD=CD,BC=12,∠ABC=60°,可得四边形ADCE是平行四边形,△ABE是等边三角形,继而求得AB=AD=CD=BE=CE=6.继而求得答案.
解答: 解:过点A作AE∥BC于点E,
解:过点A作AE∥BC于点E,
∵在梯形ABCD中,AD∥BC,
∴四边形ADCE是平行四边形,
∴AD=EC,AE=CD,
∵AB=CD,
∴AB=AE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=BE,
∵AB=AD,
∴AD=AB=CD=BE=CE=
BC=
×12=6,
∴梯形ABCD的周长为:AB+AD+CD+BC=30.
故答案为:30.
 解:过点A作AE∥BC于点E,
解:过点A作AE∥BC于点E,∵在梯形ABCD中,AD∥BC,
∴四边形ADCE是平行四边形,
∴AD=EC,AE=CD,
∵AB=CD,
∴AB=AE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=BE,
∵AB=AD,
∴AD=AB=CD=BE=CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴梯形ABCD的周长为:AB+AD+CD+BC=30.
故答案为:30.
点评:此题考查了等腰梯形的性质、等边三角形的判定与性质以及平行四边形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
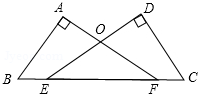 已知:如图,E是BC的中点,∠1=∠2,∠B=∠C.求证:AB=DC.
已知:如图,E是BC的中点,∠1=∠2,∠B=∠C.求证:AB=DC.