题目内容
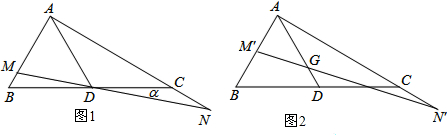
17.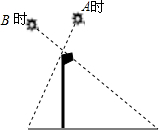 如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.
如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.
分析 如图,∠CPD=90°,QC=4m,QD=9m,利用等角的余角相等得到∠QPC=∠D,则可判断Rt△PCQ∽Rt△DPQ,然后利用相似比可计算出PQ.
解答 解: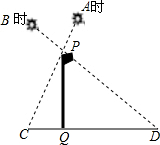 如图,∠CPD=90°,QC=4m,QD=9m,
如图,∠CPD=90°,QC=4m,QD=9m,
∵PQ⊥CD,
∴∠PQC=90°,
∴∠C+∠QPC=90°,
而∠C+∠D=90°,
∴∠QPC=∠D,
∴Rt△PCQ∽Rt△DPQ,
∴$\frac{PQ}{QD}$=$\frac{QC}{PQ}$,即$\frac{PQ}{9}$=$\frac{4}{PQ}$,
∴PQ=6,
即旗杆的高度为6m.
故答案为6.
点评 本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
15.已知b的立方根是-45.6,则立方根是456的数是( )
| A. | 100b | B. | -1000b | C. | -100b | D. | 1000b |
2.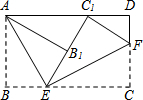 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 2 | D. | 2$\sqrt{3}$ |
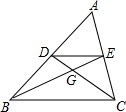 如图,点D,E分别是△ABC的边AB,AC的中点,BE交CD于G点,
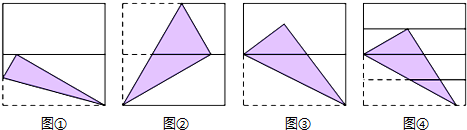
如图,点D,E分别是△ABC的边AB,AC的中点,BE交CD于G点,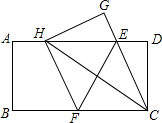 如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )
如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )