题目内容
5.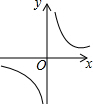 反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )
反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )| A. | 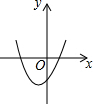 | B. | 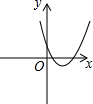 | C. | 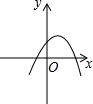 | D. | 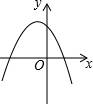 |
分析 根据反比例函数的图象得到k>0,然后根据抛物线的性质得到抛物线的开口向上,由对称轴为直线x=-$\frac{-1}{4k}$>0,得到对称轴在y轴的右侧,即可得到正确选项.
解答 解:∵反比例函数图象过第一三象限,
∴k>0,
∴抛物线的开口向上,C、D选项错误;
又∵对称轴为直线x=-$\frac{-1}{4K}$>0,
∴y=2kx2-x-k的对称轴在y轴的右侧,
所以A选项错误,B选项正确.
故选B.
点评 本题考查了二次函数y=ax2+bx+c(a≠0)的图象:当a>0,开口向上;a<0,开口向下;a与b同号,对称轴在y轴的左侧;a与b异号,对称轴在y轴的右侧;c<0,抛物线与y轴的交点在x轴下方.也考查了反比例函数的图象.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4. 如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )
如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )
 如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )
如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )| A. | 2 | B. | 4 | C. | 1.5π-2 | D. | $\frac{2π}{3}$ |
 如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.
如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数. △ABC中,∠B,∠C的平分线交于F,∠ABC=42°,∠A=60°,求∠BFC的度数.
△ABC中,∠B,∠C的平分线交于F,∠ABC=42°,∠A=60°,求∠BFC的度数.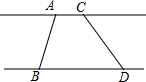 如图所示,直线a∥b且夹在两直线间的线段AB=CD,所以说夹在两平行线间的线段相等.这种说法对吗?请说明理由.
如图所示,直线a∥b且夹在两直线间的线段AB=CD,所以说夹在两平行线间的线段相等.这种说法对吗?请说明理由. 如图所示,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.
如图所示,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.