题目内容
4. 如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )
如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )| A. | 2 | B. | 4 | C. | 1.5π-2 | D. | $\frac{2π}{3}$ |
分析 连接OP、OB,把两部分的面积均可转化为规则图形的面积,不难发现两部分面积之差的绝对值即为三角形BOP的面积的2倍.
解答 解:连接OP、OB,如图所示: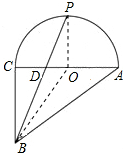
∵图形BAP的面积=△AOB的面积+△BOP的面积+扇形OAP的面积,
图形BCP的面积=△BOC的面积+扇形OCP的面积-△BOP的面积,
又∵点P是半圆弧AC的中点,OA=OC,
∴扇形OAP的面积=扇形OCP的面积,△AOB的面积=△BOC的面积,
∴两部分面积之差的绝对值是2S△BOP=OP•OC=4;
故选:B.
点评 本题考查了扇形面积的计算、三角形面积的计算;此题要能够把不规则图形的面积转化为规则图形的面积.注意根据已知条件发现面积相等的图形.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
4.关于x的不等式组$\left\{\begin{array}{l}{x-3>0}\\{x+a<2}\end{array}\right.$有2个整数解,则a的取值范围是( )
| A. | -4≤a<-3 | B. | -4<a≤-3 | C. | -5≤a<-4 | D. | -5<a≤-4 |
14.在平面直角坐标系中,点P(-2,3-π)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
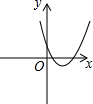
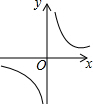 反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )
反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )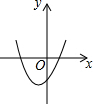
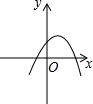
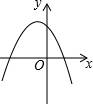
 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BF⊥CD于点F,AB交CD于点E,求证:AD=BF-DF.
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BF⊥CD于点F,AB交CD于点E,求证:AD=BF-DF.