题目内容
20. 如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.
如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.
分析 由矩形的性质得出∠C=90°,AD∥BC,由平行线的性质得出∠3=∠EFG=50°,∠EGF=∠1,由折叠的性质得:∠GDC=∠GEF=∠3=50°,∠EDC=90°,求出∠1=80°,得出∠EGF=∠1=80°,在由直角三角形的性质即可得出∠2=10°.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴∠C=90°,AD∥BC,
∴∠3=∠EFG=50°,∠EGF=∠1,
由折叠的性质得:∠GDC=∠GEF=∠3=50°,∠EDC=90°,
∴∠1=180°-50°-50°=80°,
∴∠EGF=∠1=80°,
∴∠2=90°-80°=10°.
点评 本题考查了矩形的性质、平行线的性质、折叠的性质、直角三角形的性质等知识;熟练掌握矩形的性质和折叠的性质是解决问题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
10.下列命题中,假命题是( )
| A. | 有一个角为60°的等腰三角形是等边三角形 | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 三内角之比为1:2:3的三角形是直角三角形 | |
| D. | 直角三角形的两个锐角互余 |
8.下列各式中,是完全平方式的有( )
①a2-a+$\frac{1}{4}$;②x2+xy+y;③$\frac{1}{16}$m2+m+9;④x2-xy+$\frac{1}{4}$y2;⑤m2+4n2+4mn;⑥$\frac{1}{4}$a2b2+ab+1.
①a2-a+$\frac{1}{4}$;②x2+xy+y;③$\frac{1}{16}$m2+m+9;④x2-xy+$\frac{1}{4}$y2;⑤m2+4n2+4mn;⑥$\frac{1}{4}$a2b2+ab+1.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
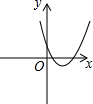
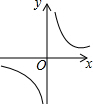 反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )
反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )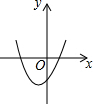
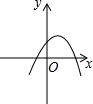
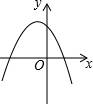
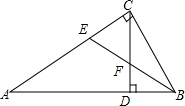 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )