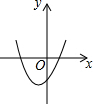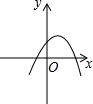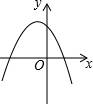题目内容
13.对于正数x,规定f(x)=$\frac{1}{1+x}$,例如f(4)=$\frac{1}{1+4}$=$\frac{1}{5}$,f(2013)+f(2012)+…+f(2)+f(1)+f($\frac{1}{2}$)+…f($\frac{1}{2012}$)+f($\frac{1}{2013}$)=2012$\frac{1}{2}$.分析 根据f(x)=$\frac{1}{1+x}$,可以把f(2013)+f(2012)+…+f(2)+f(1)+f($\frac{1}{2}$)+…f($\frac{1}{2012}$)+f($\frac{1}{2013}$)展开然后合并即可解答本题.
解答 解:∵f(x)=$\frac{1}{1+x}$,
∴f(2013)+f(2012)+…+f(2)+f(1)+f($\frac{1}{2}$)+…f($\frac{1}{2012}$)+f($\frac{1}{2013}$)
=$\frac{1}{1+2013}+\frac{1}{1+2012}+…+\frac{1}{1+2}+\frac{1}{1+1}$$+\frac{1}{1+\frac{1}{2}}+\frac{1}{1+\frac{1}{3}}+…+\frac{1}{1+\frac{1}{2012}}+\frac{1}{1+\frac{1}{2013}}$,
=$\frac{1}{1+2013}+\frac{1}{1+2012}+…+\frac{1}{1+2}+\frac{1}{1+1}$+$\frac{2}{1+2}+\frac{3}{1+3}+…+\frac{2012}{1+2012}+\frac{2013}{1+2013}$
=$(\frac{1}{1+2013}+\frac{2013}{1+2013})+(\frac{1}{1+2012}+\frac{2012}{1+2012})+…+(\frac{1}{1+2}+\frac{2}{1+2})+\frac{1}{1+1}$
=1+1+…+1+$\frac{1}{2}$
=2013-1+$\frac{1}{2}$
=2012$\frac{1}{2}$,
故答案为:2012$\frac{1}{2}$.
点评 本题考查有理数的混合运算,解题的关键是明确新定义,可以根据新定义将式子展开,观察式子的特点,计算出式子的结果.

| A. | -4≤a<-3 | B. | -4<a≤-3 | C. | -5≤a<-4 | D. | -5<a≤-4 |
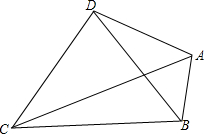 如图,四边形ABCD中,AC、BD为对角线,AC=10,BC=6,∠ADB=∠ABD=∠ACB=30°,那么线段CD的长为10$\sqrt{3}$-6.
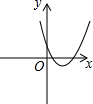
如图,四边形ABCD中,AC、BD为对角线,AC=10,BC=6,∠ADB=∠ABD=∠ACB=30°,那么线段CD的长为10$\sqrt{3}$-6.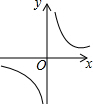 反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )
反比例函数y=$\frac{k}{x}$的图象如图,则函数y=2kx2-x+k的图象( )